Uhol medzi dvoma vektormi je uhol medzi ich chvostmi a tento uhol možno ľahko nájsť pomocou krížového súčinu a bodového súčinu vektorových vzorcov. Uhol medzi dvoma vektormi je vždy medzi 0° a 180°.

V tomto článku sa podrobne dozvieme o uhle medzi dvoma vektormi, definícii, vzorcoch a príkladoch.

Aký je uhol medzi dvoma vektormi?

Uhol medzi dvoma vektormi je uhol vytvorený v priesečníku ich chvostov. Uhol medzi dvoma vektormi môže byť ostrý, pravý alebo tupý, v závislosti od smeru vektorov.

Uhol medzi dvoma vektormi sa zistí pomocou dvoch vzorcov:

• Použitie bodového súčinu vektorov
• Použitie krížového súčinu vektorov

Toto je vysvetlené vo vzorci nižšie.

Uhol medzi dvoma vektormi vzorcov

Uhol medzi dvoma vektormi sa ľahko a najčastejšie nájde pomocou skalárneho súčinu vektorov.

Dva vektory A a B

Skalárny súčin A a B je dané,

vec{A}.vec{B} = |A| |B| cosθ.

Špeciálne prípady

• Keď je uhol medzi vektormi 0 stupňov.

To je θ = 0°

⇒ |A| |B| cosθ

⇒ |A| |B| cos0°

⇒ |A| |B| [cos0° = 1]

• Keď je uhol medzi vektormi 180 stupňov.

⇒ |A| |B| cosθ

⇒ |A| |B| cos180°

string split java

⇒ – |A| |B| [cos180° = -1]

• Keď je uhol medzi vektormi 90 stupňov.

⇒ |A| |B| cosθ

⇒ |A| |B| cos90°

⇒ |A| |B| × 0 [cos90° = 0]

⇒ 0

Vzorec pre uhol medzi dvoma vektormi

Kosínus uhla medzi dvoma vektormi sa rovná súčtu súčinu jednotlivých zložiek dvoch vektorov, delené súčinom veľkosti týchto dvoch vektorov.

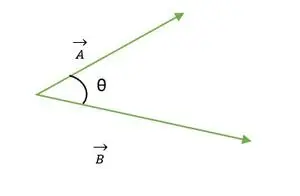
Dva vektory A a B

vec{A}.vec{B} =| A | | B | cosθ.

cosθ=frac{vec{A}.vec{B}}B

θ= cos^-1 frac{vec{A}.vec{B}}B

V karteziánskej forme,

A = A_Xi + A_aj + A_Sk

B = B_Xi + B_aj + B_Sk

cos θ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Vlastnosti produktu Dot

• Bodový súčin je komutatívny

vec{A}.vec{B}=vec{B}.vec{A}

• Dot produkt je distribučný

vec{A}.(vec{B}+vec{C})=(vec{A}.vec{B}+vec{A}.vec{C})

Uhol medzi dvoma vektormi leží medzi 0 ≤ θ ≤ 180. Keď sa konce alebo hlavy oboch vektorov zhodujú, vypočíta sa uhol medzi vektormi.

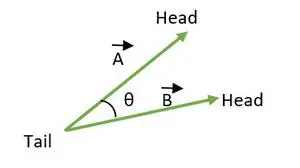
Chvost zhodný

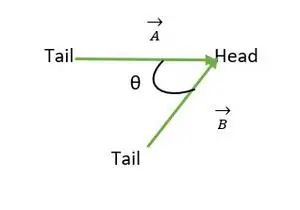
Hlava Zhoda

Vzorové problémy Uhol medzi vzorcom dvoch vektorov

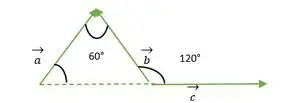
Úloha 1: Nájdite uhol medzi vektormi (ak tvoria rovnostranný trojuholník)

• a a b vektory
• b a c vektory
• a a c vektory

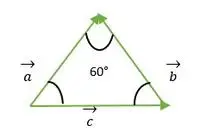
Rovnostranný trojuholník tvorený vektorom a, b, c

Riešenie:

• a a b vektory

Pre vektor a a b sa hlava oboch vektorov navzájom zhoduje, takže uhol medzi vektorom a a b je rovnaký ako uhol medzi dvoma stranami rovnostranného trojuholníka = 60°.

• vektory b a c:

Z vyššie uvedeného obrázku vidíme, že hlava alebo chvost vektora b a c sa navzájom nezhodujú.

Takže pomocou vlastnosti- A vektor zostáva nezmenený, ak je prenášaný paralelne so sebou samým.

Vektor c je posunutý rovnobežne so sebou samým

Teraz vidíme, že koniec vektorov b a c sa navzájom zhoduje, preto je rovnaký ako vonkajší uhol, ktorý zviera rovnostranný trojuholník = 120°.

• a a c vektory

Chvost a a c sa zhoduje

Pre vektory a a c sa konce oboch vektorov navzájom zhodujú, preto je uhol medzi vektormi a a c rovnaký ako uhol medzi dvoma stranami rovnostranného trojuholníka = 60°.

Úloha 2: Nájdite uhly medzi vektormi, ak tvoria rovnoramenný pravouhlý trojuholník.

• a a b vektor
• b a c vektor
• a a c vektory

Riešenie:

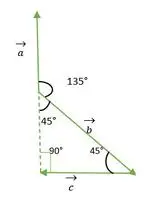
• a a b vektor

Pravý uhol Rovnoramenný trojuholník

Z vyššie uvedeného obrázku vidíme, že hlava alebo chvost vektora a a b sa navzájom nezhodujú. Takže pomocou vlastnosti- A vektor zostáva nezmenený, ak je prenášaný paralelne so sebou samým.

vektor je posunutý rovnobežne so sebou samým

Teraz sa chvosty vektorov a a b navzájom zhodujú a zvierajú uhol rovnaký ako vonkajší uhol pravouhlého rovnoramenného trojuholníka = 135°.

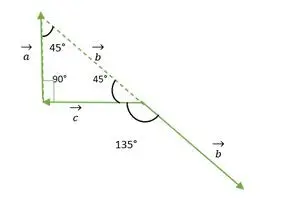
• b a c vektor

Pravý uhol Rovnoramenný trojuholník

Z vyššie uvedeného obrázku sa vektorová hlava alebo chvosty b a c navzájom nezhodujú. Takže pri použití vlastnosti zostáva vektor nezmenený, ak je prenášaný paralelne so sebou samým.

b vektor je posunutý rovnobežne so sebou samým

Teraz sa chvosty vektorov b a c navzájom zhodujú a zvierajú uhol rovnaký ako vonkajší uhol pravouhlého rovnoramenného trojuholníka = 135°.

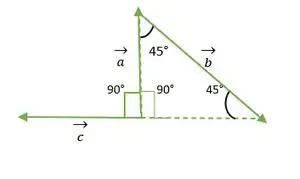
• a a c vektory

Pravý uhol Rovnoramenný trojuholník

Z vyššie uvedeného obrázku a a c vektorová hlava alebo chvosty sa navzájom nezhodujú. Takže pomocou vlastnosti- A vektor zostáva nezmenený, ak je prenášaný paralelne so sebou samým.

c vektor sa pohybuje rovnobežne so sebou samým

Teraz sa chvosty vektorov a a c navzájom zhodujú a zvierajú uhol rovnaký ako pravý uhol rovnoramenného trojuholníka = 90°.

Úloha 3: Nájdite uhol medzi vektormi A = i + j + k a vektorom B = -2i – 2j – 2k.

Riešenie:

Zo vzorca,

A = A_Xi + A_aj + A_Sk

B = B_Xi + B_aj + B_Sk

cosθ=frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Tu v danej otázke

A = i + j + k

B = -2i -2j -2k

Nahradenie hodnôt vo vzorci

⇒ cosθ =frac{(1.(-2)+1.(-2)+1.(-2))}{(sqrt{1^2+1^2+1^2}×sqrt{(-2)^2+(-2)^2+(-2)^2})}

⇒ cosθ =frac{(-2-2-2)}{(sqrt{1+1+1}×sqrt{4+4+4})}

⇒ cosθ =frac{-6}{(sqrt{3}×sqrt{12})}

⇒ cosθ =frac{-6}{(sqrt{36})}

⇒ cosθ = -6/6

⇒ cosθ= -1

⇒ 6 = 180°

Úloha 4: Nájdite uhol medzi vektorom A = 3i + 4j a B = 2i + j

Riešenie:

A = A_Xi + A_aj + A_Sk

B = B_Xi + B_aj + B_Sk

cosθ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Tu vzhľadom,

A = 3i + 4j + 0k

B= 2i + j + 0k

Nahradením hodnôt vo vzorci,

⇒ cosθ =frac{(3.2+4.1+0.0)}{(sqrt{3^2+4^2+0^2}×sqrt{2^2+1^2+0^2})}

⇒ cosθ =frac{(6+4+0)}{(sqrt{9+16+0}×sqrt{4+1+0})}

⇒ cosθ =frac{(10)}{(sqrt{25}×sqrt{5})}

⇒ cosθ =frac{(10)}{(sqrt{125})}

⇒ θ = cos^-1(frac{(10)}{5.(sqrt{5})})

⇒ θ = cos^-1(frac{2}{(sqrt{5})})

Úloha 5: Nájdite uhol medzi vektorom A = i + j a vektorom B = j + k.

Riešenie:

Zo vzorca,

A = A_Xi + A_aj + A_Sk

B = B_Xi + B_aj + B_Sk

cosθ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Tu v danej otázke

⇒ A = i + j

⇒ B = j + k

⇒ cosθ =frac{(1.0+1.1+0.1)}{(sqrt{1^2+1^2+0^2}×sqrt{0^2+1^2+1^2})}

⇒ cosθ =frac{(1)}{(sqrt{1+1+0}×sqrt{0+1+1})}

⇒ cosθ =frac{1}{(sqrt{2}×sqrt{2})}

⇒ θ = cos^-1(1/2)

⇒ 6 = 60°