Hranol je trojrozmerná pevná postava s dvoma rovnakými koncami. Skladá sa z plochých strán, podobných základov a rovnakých prierezov. Jeho plochy sú rovnobežníky alebo obdĺžniky bez základne. Taký hranol, ktorý má tri pravouhlé plochy a dve rovnobežné trojuholníkové základne, sa nazýva trojuholníkový hranol. Trojuholníkové základne sú spojené bočnými plochami, ktoré prebiehajú navzájom paralelne.

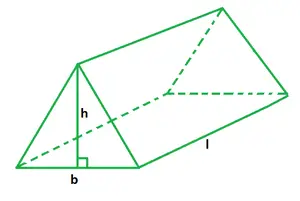
Objem vzorca s trojuholníkovým hranolom

Objem trojuholníkového hranola je definovaný ako priestor vo vnútri alebo priestor, ktorý vypĺňa. Na výpočet jeho objemu stačí poznať základnú plochu a výšku trojuholníkového hranolu. Objem trojuholníkového hranola sa rovná súčinu plochy základne a výšky hranola, známej aj ako dĺžka hranola. Plocha základne trojuholníkového hranola sa rovná polovici súčinu trojuholníkovej základne a jej nadmorskej výšky.

Vzorec

V = (1/2) × b × v × l

kde,

b je trojuholníková základňa,

h je výška hranola,

l je dĺžka hranola.

Vzorové problémy

Úloha 1. Nájdite objem trojuholníkového hranolu, ak má základňu 6 cm, nadmorskú výšku 8 cm a dĺžku 12 cm.

Riešenie:

Máme b = 6, h = 8 a l = 12.

klauzuly sql

Pomocou vzorca, ktorý máme,

V = (1/2) × b × v × l

= (1/2) × 6 × 8 × 12

= 3 × 8 × 12

= 288 cu. cm

Úloha 2. Nájdite objem trojuholníkového hranolu, ak má základňu 5 cm, nadmorskú výšku 7 cm a dĺžku 8 cm.

previesť reťazec na char java

Riešenie:

Máme b = 5, h = 7 a l = 8.

Pomocou vzorca, ktorý máme,

V = (1/2) × b × v × l

= (1/2) × 5 × 7 × 8

= 5 × 7 × 4

= 140 cu. cm

Úloha 3. Nájdite dĺžku trojuholníkového hranolu, ak má základňu 6 cm, nadmorskú výšku 9 cm a objem 98 cu. cm.

Riešenie:

Máme b = 6, h = 9 a V = 98.

Pomocou vzorca, ktorý máme,

V = (1/2) × b × v × l

=> 98 = (1/2) × 6 × 9 × l

koľko rokov má kylie jenner

=> 196 = 27 l

=> l = 196/27

=> l = 7,25 cm

Úloha 4. Nájdite výšku trojuholníkového hranola, ak je jeho základňa 8 cm, dĺžka 14 cm a objem 504 cu. cm.

Riešenie:

Máme, b = 8, l = 14 a V = 504.

Pomocou vzorca, ktorý máme,

V = (1/2) × b × v × l

=> 504 = (1/2) × 8 × v × 14

=> 504 = 56 h

=> h = 504/56

=> v = 9 cm

Úloha 5. Nájdite plochu podstavy trojuholníkového hranolu, ak je jeho dĺžka 18 cm, výška 10 cm a objem 450 cu. cm.

Riešenie:

Máme, l = 18, h = 10 a V = 450.

Pomocou vzorca pre objem, ktorý máme,

V = (1/2) × b × v × l

=> 450 = (1/2) × b × 10 × 18

=> 450 = 90b

=> b = 450/90

=> b = 5 cm

Plocha trojuholníkovej základne je teda

linuxová architektúra

A = (1/2) × b × h

= (1/2) × 5 × 10

= 25 cm2