Objem trojuholníkovej pyramídy sa zistí pomocou vzorca V = 1/3 A.H . Trojuholníková pyramída, tiež známa ako štvorsten, je typ pyramídy s trojuholníkovou základňou a tromi trojuholníkovými plochami, ktoré sa stretávajú v jednom bode nazývanom vrchol.

V tomto článku sa podrobne dozvieme o definícii pyramídy, definícii trojuholníkovej pyramídy, vzorci trojuholníkovej pyramídy, príkladoch a ďalších.

Obsah

• Čo je pyramída?
• Definícia trojuholníkovej pyramídy
• Vzorec trojuholníkovej pyramídy
• Povrchová plocha trojuholníkovej pyramídy
• Objem trojuholníkovej pyramídy

Čo je pyramída?

A pyramída sa delí na rôzne druhy na základe tvaru podstavy, ako je trojuholníková pyramída, štvorcová pyramída, päťuholníková pyramída, šesťuholníková pyramída atď. Vrchol je bod stretnutia bočných plôch alebo bočných plôch pyramídy. . Kolmá vzdialenosť od vrcholu pyramídy k stredu jej základne je výška alebo nadmorská výška pyramídy. Kolmá vzdialenosť medzi vrcholom a základňou bočného povrchu šikmej výšky pyramídy.

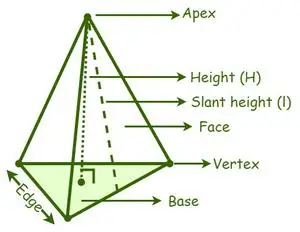
Pyramída

Definícia trojuholníkovej pyramídy

Trojuholníková pyramída je pyramída, ktorej základňou je trojuholník. Je tiež známy ako štvorsten a má tri trojuholníkové plochy a jednu trojuholníkovú základňu, pričom trojuholníková základňa môže byť skalárna, rovnoramenná alebo rovnostranný trojuholník. Trojuholníkový sa ďalej delí na tri typy, t. j. pravidelnú trojuholníkovú pyramídu, nepravidelnú trojuholníkovú pyramídu a pravú trojuholníkovú pyramídu.

• Pravidelná trojuholníková pyramída: Trojuholníková pyramída, ktorej štyri strany sú rovnostranné trojuholníky, sa nazýva pravidelná trojuholníková pyramída. Keďže pyramída je tvorená rovnostrannými trojuholníkmi, veľkosť všetkých jej vnútorných uhlov je 60°.

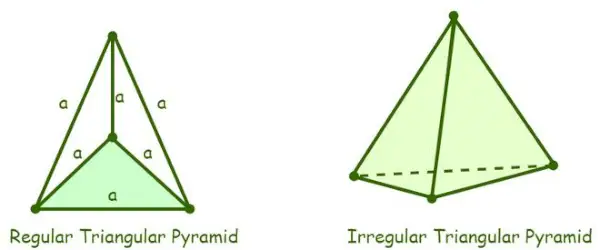
Definícia trojuholníkovej pyramídy

• Nepravidelná trojuholníková pyramída: Nepravidelná trojuholníková pyramída je taká, ktorej okraje základne nie sú rovnaké, t. j. základňa nepravidelnej trojuholníkovej pyramídy je buď zmenšený trojuholník, alebo rovnoramenný trojuholník. Všetky trojuholníkové pyramídy sa považujú za pravidelné trojuholníkové pyramídy, pokiaľ nie je trojuholníková pyramída špecificky uvedená ako nepravidelná.

• Pravá trojuholníková pyramída: Pravá trojuholníková pyramída je taká, ktorej základňa je pravouhlý trojuholník a ktorej vrchol je zarovnaný nad stredom základne.

Vzorec trojuholníkovej pyramídy

Pre trojuholníkovú pyramídu existujú dva vzorce: povrchová plocha trojuholníkovej pyramídy a objem trojuholníkovej pyramídy.

• Povrchová plocha trojuholníkovej pyramídy
  • Bočný povrch trojuholníkovej pyramídy
  • Celková plocha trojuholníkovej pyramídy
• Objem trojuholníkovej pyramídy

Povrchová plocha trojuholníkovej pyramídy

Plocha pyramídy má dva typy plôch, a to: bočnú plochu a celkovú plochu, kde plocha pyramídy je súčtom plôch bočných plôch alebo bočných plôch a základnej plochy. pyramídy.

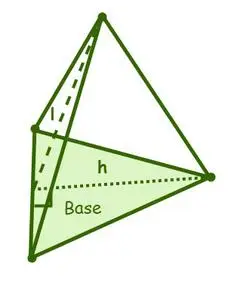
Povrchová plocha trojuholníkovej pyramídy

Bočný povrch trojuholníkovej pyramídy

Bočný povrch trojuholníkovej pyramídy sa vypočíta podľa vzorca:

Bočný povrch trojuholníkovej pyramídy (LSA) = ½ × obvod × výška sklonu

Celková plocha trojuholníkovej pyramídy

Celková plocha pyramídy (TSA) = bočná plocha pyramídy + plocha základne

Takže TSA = ½ × obvod × výška sklonu + ½ × základňa × výška

Celková plocha trojuholníkovej pyramídy (TSA) = ½ × P × l + ½ bh

kde,

• P je obvod základne
• l je šikmá výška pyramídy
• b je Základňa trojuholníka na základni
• h je výška pyramídy

Objem trojuholníkovej pyramídy

Objem pyramídy je celkový priestor uzavretý medzi všetkými stranami pyramídy. Objem pyramídy je vo všeobecnosti reprezentovaný písmenom V a jeho vzorec sa rovná jednej tretine súčinu základnej plochy a výšky pyramídy.

Vzorec pre objem pyramídy je uvedený takto:

Objem trojuholníkovej pyramídy = 1/3 × základná plocha × výška

V = 1/3 × AH kubických jednotiek

kde,

• V je objem pyramídy
• A je oblasť základne pyramídy
• H je výška alebo nadmorská výška pyramídy

Vzorec pre objem pravidelnej trojuholníkovej pyramídy je uvedený nasledovne

Objem pravidelnej trojuholníkovej pyramídy = a ³ /6√2 kubických jednotiek

Kde a je Dĺžka hrán

Atikel súvisiaci s trojuholníkovou pyramídou:

• Obdĺžniková pyramída
• Štvorcová pyramída
• Päťuholníková pyramída
• Šesťhranná pyramída
• Objem pyramídového vzorca
• Povrchová plocha pyramídového vzorca

Príklady vzorca pre trojuholníkovú pyramídu

Príklad 1: Určte objem trojuholníkového ihlana, ktorého základná plocha a výška sú 50 cm ² a 12 cm.

Riešenie:

Vzhľadom na údaje,

• Plocha trojuholníkovej základne = 100 cm²
• Výška pyramídy = 12 cm

My to vieme,

Objem trojuholníkového ihlana (V) = 1/3 × Plocha trojuholníkovej základne × Výška

V = 1/3 × 50 × 12 = 200 cm³

Objem danej trojuholníkovej pyramídy je teda 200 cm³.

Príklad 2: Nájdite celkový povrch pravidelnej trojuholníkovej pyramídy, keď je dĺžka každej hrany 8 palcov.

Riešenie:

Vzhľadom na údaje,

• Dĺžka každého okraja pravidelného trojuholníkového ihlana (a) = 8 palcov

My to vieme,

Celková plocha pravidelného trojuholníkového ihlana = √3a²

⇒ TSA = √3 × 8²

= 64√3 = 110,851 štvorcových palcov

Celková plocha pravidelnej trojuholníkovej pyramídy je teda 110 851 štvorcových palcov.

Príklad 3: Určte objem pravidelného trojuholníkového ihlanu, keď je dĺžka hrany 10 cm.

Riešenie:

Vzhľadom na údaje,

• Dĺžka každej hrany pravidelného trojuholníkového ihlanu (a) = 10 cm

My to vieme,

Objem pravidelného trojuholníkového ihlana = a³/6√2

⇒ V = (10)³/6√2

= 1000/6√2 = 117,85 cm³

Objem pravidelnej trojuholníkovej pyramídy je teda 117,85 cu. cm.

Príklad 4: Nájdite výšku sklonu trojuholníkovej pyramídy, ak je jej bočný povrch 600 štvorcových palcov a obvod základne je 60 palcov.

Riešenie:

Vzhľadom na údaje,

• Bočný povrch = 600 štvorcových palcov
• Obvod základne = 60 palcov

My to vieme,

Bočný povrch = ½ × obvod × výška sklonu

600 = ½ × 60 × l

l = 600/30 = 20 palcov

Výška sklonu danej pyramídy je teda 20 palcov.

Príklad 5: Určte celkový povrch trojuholníkového ihlana, ktorého základná plocha je 28 cm2, obvod trojuholníka je 18 cm a výška pyramídy je 20 cm.

Riešenie:

Vzhľadom na údaje,

• Plocha trojuholníkovej základne = 28 cm²
• Výška sklonu (l) = 20 cm
• Obvod (P) = 18 cm

My to vieme,

Celková plocha povrchu (TSA) trojuholníkovej pyramídy = ½ × obvod × výška sklonu + plocha základne

⇒ TSA = ½ × 18 × 20 + 28

= 180 + 28 = 208 cm2

generátor náhodných hodnôt v jave

Celková plocha danej pyramídy je teda 208 cm2.

Cvičte problémy na vzorci trojuholníkovej pyramídy

Q1. Aký je objem pyramídy pri trojuholníkovej pyramíde so základnou plochou 15 štvorcových jednotiek a výškou 10 jednotiek?

Q2. Aká je celková plocha pyramídy pri pravidelnej trojuholníkovej pyramíde s každou hranou rovnostrannej trojuholníkovej základne meranou 6 jednotiek?

Q3. Aký je objem a celkový povrch pyramídy pri pravidelnej trojuholníkovej pyramíde s každou hranou rovnostrannej trojuholníkovej základne meranou 4 jednotky a výškou 5 jednotiek?

Q4. Ak sú dĺžky strán základne trojuholníkovej pyramídy 3 jednotky, 4 jednotky a 5 jednotiek a výška pyramídy je 12 jednotiek, aký je objem pyramídy?

Q5. Aká je celková plocha pre trojuholníkovú pyramídu so základňou v tvare pravouhlého trojuholníka s nohami 3 a 4 jednotky a preponou 5 jednotiek, ak je výška pyramídy od základne po vrchol 10 jednotiek ?

Časté otázky o vzorci trojuholníkovej pyramídy

Aká je definícia trojuholníkovej pyramídy?

Trojuholníková pyramída je geometrický tvar, ktorý má trojuholníkovú základňu a tri trojuholníkové steny so spoločným vrcholom.

Koľko plôch a vrcholov má trojuholníková pyramída?

Trojuholníková pyramída má štyri steny a štyri vrcholy. Jeden vrchol je spoločný pre všetky tri strany pyramídy.

Čo je základný vzorec pre pyramídu?

Základné vzorce pyramídy sú:

• LSA = ½ × obvod × výška sklonu
• TSA = ½ × P × l + ½ bh
• V = 1/3 x AH

Aké sú typy trojuholníkových pyramíd?

Existujú tri typy trojuholníkových pyramíd

• Pravidelná trojuholníková pyramída
• Nepravidelná trojuholníková pyramída
• Pravoúhlá trojuholníková pyramída

Čo je vzorec pre trojuholníky?

Vzorec pre obsah trojuholníka je:

• (Plocha)A = 1/2 × b × h