V tomto článku sa budeme zaoberať prechodom cez strom v dátovej štruktúre. Pojem „prechádzanie stromom“ znamená prechádzanie alebo navštevovanie každého uzla stromu. Existuje jeden spôsob, ako prejsť lineárnou dátovou štruktúrou, ako je napríklad prepojený zoznam, front a zásobník. Existuje niekoľko spôsobov, ako prechádzať stromom, ktoré sú uvedené nasledovne -

• Prechod predobjednávky
• Neriadkový prechod
• Prenos poštovej poukážky

Takže v tomto článku budeme diskutovať o vyššie uvedených technikách prechádzania stromom. Teraz začnime diskutovať o spôsoboch prechodu stromov.

Prechod predobjednávky

Táto technika sa riadi zásadou „koreň zľava doprava“. To znamená, že najprv sa navštívi koreňový uzol, potom sa rekurzívne prejde ľavý podstrom a nakoniec sa rekurzívne prejde pravý podstrom. Keďže koreňový uzol prechádza pred (alebo pred) ľavým a pravým podstromom, nazýva sa to prechod pred poradím.

Takže pri prechode predobjednávky je každý uzol navštívený pred oboma jeho podstrommi.

Aplikácie prechodu predobjednávky zahŕňajú -

• Používa sa na vytvorenie kópie stromu.
• Môže sa použiť aj na získanie predponového výrazu stromu výrazov.

Algoritmus

 Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively. 

Príklad

Teraz sa pozrime na príklad techniky prechodu predobjednávky.

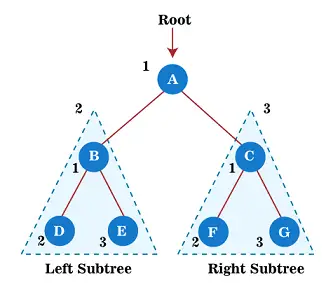
Teraz začnite aplikovať prechod predobjednávky na strom vyššie. Najprv prejdeme koreňový uzol A; potom sa presuňte do jeho ľavého podstromu B , ktorý sa bude prechádzať aj v predobjednávke.

Takže pre ľavý podstrom B najprv koreňový uzol B sa prechádza sám; potom jeho ľavý podstrom D je prejdená. Od uzla D nemá žiadne deti, presuňte sa do pravého podstromu A . Keďže uzol E tiež nemá žiadne potomky, prechod ľavého podstromu koreňového uzla A je dokončený.

nastaviť java

Teraz sa posuňte smerom k pravému podstromu koreňového uzla A, ktorý je C. Takže pre pravý podstrom C najprv koreňový uzol C prešiel sám; potom jeho ľavý podstrom F je prejdená. Od uzla F nemá žiadne deti, presuňte sa do pravého podstromu G . Keďže uzol G tiež nemá žiadne potomky, prechod pravého podstromu koreňového uzla A je dokončený.

Preto sa prechádzajú všetky uzly stromu. Takže výstup prechodu predobjednávky vyššie uvedeného stromu je -

A → B → D → E → C → F → G

Ak sa chcete dozvedieť viac o prechode predobjednávky v dátovej štruktúre, kliknite na odkaz Prechod predobjednávky .

Prenos poštovej poukážky

Táto technika sa riadi zásadou „ľavý-pravý koreň“. To znamená, že sa prejde prvý ľavý podstrom koreňového uzla, potom sa rekurzívne prejde pravý podstrom a nakoniec sa prejde koreňový uzol. Keďže koreňový uzol prechádza po (alebo po) ľavom a pravom podstrome, nazýva sa to prechod postorderom.

Takže pri prechode postorderom sa každý uzol navštívi po oboch jeho podstromoch.

Aplikácie postorder traversal zahŕňajú -

• Používa sa na odstránenie stromu.
• Môže sa použiť aj na získanie postfixového výrazu stromu výrazov.

Algoritmus

 Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node. 

Príklad

avl strom

Teraz sa pozrime na príklad techniky postorder traversal.

Teraz začnite aplikovať postorder traversal na vyššie uvedenom strome. Najprv prejdeme ľavý podstrom B, ktorým sa bude prechádzať v postorderi. Potom prejdeme pravým podstromom C v postorderi. A nakoniec, koreňový uzol vyššie uvedeného stromu, t.j. A , je prejdená.

Takže pre ľavý podstrom B najprv jeho ľavý podstrom D je prejdená. Od uzla D nemá žiadne deti, prejdite cez pravý podstrom A . Keďže uzol E tiež nemá žiadne deti, presuňte sa do koreňového uzla B. Po prechode uzlom B, prechod ľavého podstromu koreňového uzla A je dokončený.

reťazec na char v jazyku Java

Teraz sa posuňte smerom k pravému podstromu koreňového uzla A, ktorý je C. Takže pre pravý podstrom C najprv jeho ľavý podstrom F je prejdená. Od uzla F nemá žiadne deti, prejdite cez pravý podstrom G . Keďže uzol G tiež nemá žiadne potomky, napokon koreňový uzol pravého podstromu, t.j. C, je prejdená. Prechod pravého podstromu koreňového uzla A je dokončený.

Nakoniec prejdite koreňový uzol daného stromu, t.j. A . Po prejdení koreňového uzla sa dokončí postorderový prechod daného stromu.

Preto sa prechádzajú všetky uzly stromu. Takže výstup postorderového prechodu vyššie uvedeného stromu je -

D → E → B → F → G → C → A

Ak sa chcete dozvedieť viac o prechode postorderom v dátovej štruktúre, môžete kliknúť na odkaz Prenos poštovej poukážky .

Neriadkový prechod

Táto technika sa riadi zásadou „ľavý koreň vpravo“. To znamená, že po prechode koreňového uzla sa navštívi prvý ľavý podstrom a nakoniec sa prejde pravý podstrom. Keďže koreňový uzol prechádza medzi ľavým a pravým podstromom, nazýva sa prechodom bez poradia.

Takže pri prechode v poradí je každý uzol navštívený medzi svojimi podstromami.

Aplikácie Inorder traversal zahŕňajú -

• Používa sa na získanie uzlov BST v rastúcom poradí.
• Môže sa použiť aj na získanie predponového výrazu stromu výrazov.

Algoritmus

pokračovacie dátové typy

 Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively. 

Príklad

Teraz sa pozrime na príklad techniky Inorder traversal.

Teraz začnite aplikovať prechod na vyššie uvedený strom. Najprv prechádzame ľavým podstromom B ktoré sa budú prechádzať v poradí. Potom prejdeme koreňový uzol A . A nakoniec ten správny podstrom C sa prechádza v poradí.

Takže pre ľavý podstrom B , najprv jeho ľavý podstrom D je prejdená. Od uzla D nemá žiadne deti, takže po jej prejdení uzol B bude prechádzať a nakoniec pravý podstrom uzla B, tj A , je prejdená. Uzol E tiež nemá žiadne deti; preto je prechod ľavého podstromu koreňového uzla A dokončený.

Potom prejdite koreňový uzol daného stromu, t.j. A .

Nakoniec sa posuňte smerom k pravému podstromu koreňového uzla A, ktorý je C. Takže pre pravý podstrom C; najprv jeho ľavý podstrom F je prejdená. Od uzla F nemá žiadne deti, node C bude prechádzať a nakoniec pravý podstrom uzla C, tj. G , je prejdená. Uzol G tiež nemá žiadne deti; preto je prechod pravého podstromu koreňového uzla A dokončený.

Keď sa prejdú všetky uzly stromu, ukončí sa prechod v poradí daného stromu. Výstupom prechodu podľa vyššie uvedeného stromu je -

D → B → E → A → F → C → G

Ak sa chcete dozvedieť viac o prechode poradia v dátovej štruktúre, môžete kliknúť na odkaz Inorder Traversal .

Zložitosť techník prechodu cez strom

Časová zložitosť techník prechádzania stromami diskutovaná vyššie je O(n) , kde 'n' je veľkosť binárneho stromu.

Zatiaľ čo priestorová zložitosť techník prechádzania stromami diskutovaná vyššie je O(1) ak neberieme do úvahy veľkosť zásobníka pre volania funkcií. Inak je priestorová náročnosť týchto techník O(h) , kde 'h' je výška stromu.

Implementácia Tree traversal

Teraz sa pozrime na implementáciu vyššie diskutovaných techník pomocou rôznych programovacích jazykov.

Program: Napíšte program na implementáciu techník prechodu cez strom v C.

 #include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
 The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
 The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
 The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } 

Výkon

Program: Napíšte program na implementáciu techník prechodu cez strom v C#.

 using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } 

Výkon

Program: Napíšte program na implementáciu techník prechodu cez strom v C++.

 #include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node-&gt;element = val; Node-&gt;left = NULL; Node-&gt;right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout&lt;<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root-&gt;left); cout&lt;<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root-&gt;right); cout&lt;<' '<element<left="createNode(28);" root->right = createNode(48); root-&gt;left-&gt;left = createNode(23); root-&gt;left-&gt;right = createNode(33); root-&gt;left-&gt;left-&gt;left = createNode(13); root-&gt;left-&gt;left-&gt;right = createNode(26); root-&gt;right-&gt;left = createNode(43); root-&gt;right-&gt;right = createNode(58); root-&gt;right-&gt;right-&gt;left = createNode(53); root-&gt;right-&gt;right-&gt;right = createNode(68); cout&lt;<'
 the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
 inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + &apos; &apos;); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + &apos; &apos;); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + &apos; &apos;); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println(&apos;The Preorder traversal of given binary tree is - &apos;); pt.traversePreorder(); System.out.println(&apos;
&apos;); System.out.println(&apos;The Inorder traversal of given binary tree is - &apos;); pt.traverseInorder(); System.out.println(&apos;
&apos;); System.out.println(&apos;The Postorder traversal of given binary tree is - &apos;); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that&apos;s all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'>

Výkon

Po vykonaní vyššie uvedeného kódu bude výstupom -

porovnávanie reťazcov java

Záver

V tomto článku sme diskutovali o rôznych typoch techník prechodu cez strom: prechod pred poradím, prechod mimo poriadku a prechod postorder. Tieto techniky sme videli spolu s algoritmom, príkladom, zložitosťou a implementáciou v C, C++, C# a java.

Tak, to je o článku všetko. Dúfam, že to bude pre vás užitočné a poučné.