The Časová zložitosť z Merge Sort je O(n log n) v oboch priemer a najhoršie prípady . Priestorová zložitosť Zlúčiť triedenie je O(n) . 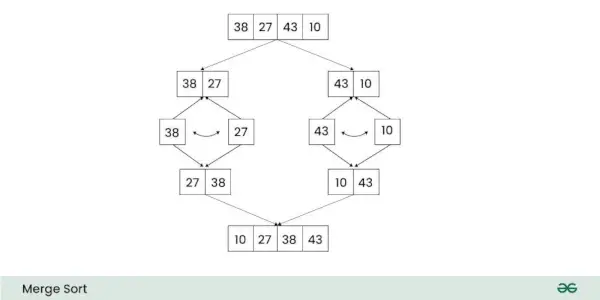
znak na reťazec java
| Aspekt | Zložitosť |
|---|---|
| Časová zložitosť | O(n log n) |
| Priestorová zložitosť | O(n) |
Analýza časovej zložitosti zoradenia zlúčenia:
Zvážte nasledujúce terminológie:
T(k) = čas potrebný na zoradenie k prvkov
M(k) = čas potrebný na zlúčenie k prvkov
Takže sa to dá napísať
T(N) = 2 * T(N/2) + M(N)
= 2 * T(N/2) + konštanta * N
Tieto N/2 prvky sa ďalej delia na dve polovice. takže,
T(N) = 2 * [2 * T(N/4) + konštanta * N/2] + konštanta * N
= 4 * T(N/4) + 2 * N * konštanta
. . .
= 2k* T(N/2k) + k * N * konštanta
Môže sa rozdeliť maximálne, kým nezostane jeden prvok. Takže, potom N/2k= 1. k = log 2 N
anotácie jarných topánok
T(N) = N* T(1) + N* log2N * konštantná
= N + N * log2N
Preto je časová zložitosť O(N * log 2 N) .
Časová náročnosť je teda v najlepšom prípade, najhoršom prípade a priemernom prípade rovnaká.
Analýza priestorovej zložitosti zoradenia zlučovania:
Zlúčiť triedenie má priestorovú zložitosť z O(n) . Je to preto, že používa pomocné pole veľkosti n na zlúčenie zoradených polovíc vstupného poľa. Pomocné pole sa používa na uloženie zlúčeného výsledku a vstupné pole sa prepíše zoradeným výsledkom.
