Pre akýkoľvek objekt, ktorý vidíte alebo sa ho môžete dotknúť, možno merať tri rozmery, dĺžku, šírku a výšku. Náš dom, v ktorom žijeme, má určité rozmery. Obdĺžniková obrazovka/monitor, na ktorý sa pozeráte, má šírku a šírku svojej dĺžky. Pre každú trojrozmernú geometrickú štruktúru sa meria plocha a objem.
Aera pokrytá povrchom objektu je plocha povrchu akéhokoľvek daného objektu. Zatiaľ čo množstvo priestoru dostupného v objekte je objem.
Obsah
- Plocha povrchu
- Celková plocha povrchu
- Zakrivená plocha/plocha bočnej plochy
- Objem
- Príklady povrchových plôch a objemov
- Časté otázky o vzorcoch plochy a objemu
Plocha povrchu
Plochu a objem povrchu je možné vypočítať pre akýkoľvek trojrozmerný (3D) geometrický tvar. Povrch akejkoľvek oblasti je oblasť, ktorú zaberá povrch objektu. Objem je množstvo priestoru dostupného v objekte. Máme rôzne typy tvarov ako polguľa, guľa, kocka, kváder, valec atď. Všetky trojrozmerné tvary majú plochu a objem. Ale dva – rozmerné tvary ako štvorce, obdĺžniky, trojuholníky, kruhy atď.
Tu v dvojrozmernom prevedení môžeme merať iba plochu. Plocha, ktorú zaberá trojrozmerný objekt jeho vonkajším povrchom, sa nazýva povrchová plocha. Meria sa v štvorcových jednotkách.
Oblasť je dvoch typov:
- Celková plocha povrchu
- Zakrivená plocha/plocha bočnej plochy
Celková plocha povrchu
Plocha zahŕňajúca základňu (základne) a zakrivenú časť zodpovedá celkovej ploche povrchu. Je to veľkosť plochy ohraničenej povrchom objektu. Ak má formulár zakrivenú základňu a povrch, tak súčet dvoch oblastí bude celková plocha. Celková plocha povrchu môže byť definovaná ako celková plocha pokrytá objektom vrátane jeho základne, ako aj zakrivenej časti. Ak má objekt základnú aj zakrivenú plochu, potom sa celková plocha povrchu bude rovnať súčtu základnej a zakrivenej plochy.
- Celková plocha je celková plocha, ktorú zaberá objekt.
- Vezmime si napríklad kváder ako príklad, kváder má 6 plôch, 12 hrán a 8 vrcholov.
Celková plocha = základná plocha + zakrivená plocha
python os zoznam
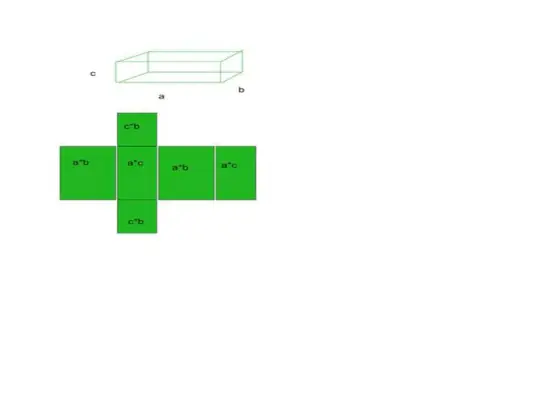
- Súčet všetkých týchto 6 oblastí bude naša celková plocha konkrétneho tvaru
Príklad:
Nižšie je uvedený kváder, ktorého rozmer je daný ako dĺžka = 8 cm, šírka = 4 cm a výška = 6 cm, nájdite TSA kvádra
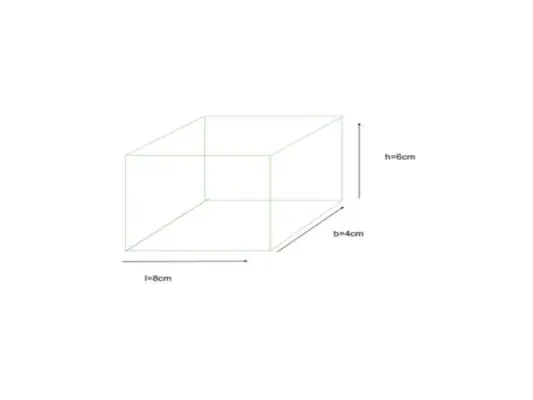
dané l = 8 cm, b = 4 cm, v = 6 cm
TSA = 2((l * b) + (l * h) + (b * h))
= 2((8 * 4) + (8 * 6) + (4 * 6))
= 2((32) + (48) + (24))
= 2 (104)
= 208
TSA kvádra je 208 cm.
Zakrivená plocha/plocha bočnej plochy
Zakrivený povrch, okrem jeho stredu, zodpovedá ploche iba zakrivenej časti tvaru (tvarov). Pre tvary, ako je kužeľ, sa často nazýva plocha bočného povrchu. Bočná povrchová plocha môže byť definovaná ako oblasť, ktorá zahŕňa len zakrivenú povrchovú plochu objektu alebo laterálnu povrchovú plochu objektu vylúčením základnej plochy objektu. Oblasť laterálneho povrchu je tiež známa ako oblasť zakriveného povrchu.
Väčšina tvarov alebo objektov sa vzťahuje na zakrivenú plochu povrchu, tvar alebo valec podobný objektu sa na ňu vzťahuje ako na oblasť bočnej plochy. Jednoducho povedané, oblasť, ktorá je pre nás viditeľná, sa nazýva bočná plocha. Uvažujme napríklad valec, ako je znázornené na obrázku nižšie.
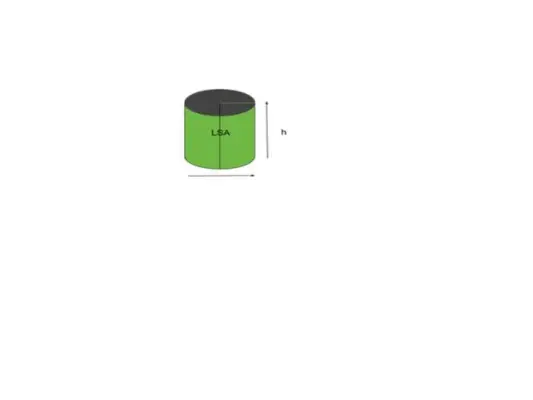
Objem
Objem je množstvo priestoru v určitom 3D objekte. Celkové množstvo priestoru, ktorý predmet alebo látka zaberá, sa nazýva objem. Meria sa v kubických jednotkách.
Vzorce pre povrchovú plochu a objem
Uvedená tabuľka obsahuje celkovú plochu povrchu, zakrivenú plochu povrchu/plochu bočného povrchu a objem rôznych tvarov.
| Názov tvaru | Zakrivená plocha povrchu | Celková plocha povrchu | Objem |
|---|---|---|---|
| Kváder | 2 h (l + b) | 2 (lb + bh + hl) | l * b * h |
| Kocka | 4a2 | 6a2 | a3 |
| Valec | 2πrh | 2π(r + h) | πr2h |
| Sphere | 4πr2 mycricketlive | 4πr2 | 4/3π r3 |
| Kužeľ | πrl | πr(r + l) | 1/3π r2h |
| Hemisféra | 2pr2 | 3πr2 | 2/3π r3 |
Čítaj viac:
- Povrchová plocha pyramídy
- Povrchová plocha valca
- Povrchová plocha pologule
- Povrchová plocha sféry
- Povrchová plocha kvádra
Príklady povrchových plôch a objemov
Príklad 1: 2 kocky každá s objemom 512 cm 3 sú spojené koncami. Nájdite povrch výsledného kvádra?
Riešenie:
Vzhľadom na to,
Objem (V) každej kocky je = 512 cm3
teraz môžeme naznačiť, že a3= 512 cm3
∴ Strana kocky, t.j. a = 8 cm
Teraz bude šírka a dĺžka výsledného kvádra 8 cm a jeho výška 16 cm.
Takže plocha kvádra (TSA) = 2 (lb + bh + lh)
Teraz, uvedením hodnôt, dostaneme,
= 2 (8 × 16 + 8 × 8 + 16 × 8) cm 2
= (2 × 320) = 640 cm 2
Z toho vyplýva, že TSA kvádra = 640 cm 2
Príklad 2: Máme valcovú sviečku s priemerom 14 cm a dĺžkou 2 cm. Roztaví sa do tvaru kvádra sviečky s rozmermi 7 cm × 11 cm × 1 cm. Koľko kvádrových sviečok možno získať?
Riešenie:
Rozmery cylindrickej sviečky:
Polomer valcovej sviečky = 14/2 cm = 7 cm
Výška/hrúbka = 2 cm
Objem jednej valcovej sviečky = πr2h = π x 7 x 7 x (2) cm3= 308 cm3.
Objem kvádra sviečka = 7 x 11 x 1 = 77 cm3
Preto počet kvádrových sviečok = objem kvádrovej sviečky/objem jednej valcovej sviečky = 308/77 = 4
Takto môžeme získať 4 sviečky v tvare kvádra.
Príklad 3: Žena chce postaviť guľovú hračku z hliny, ktorej polomer sa rovná polomeru náramku, ktorý nosí. Vzhľadom na to, že náramok má kruhový tvar, chce tiež, aby sa plocha náramku rovnala objemu gule. Zistite polomer náramku, ktorý nosí?
Riešenie:
Nech r je polomer náramku aj gule,
Bolo nám dané, že objem gule sa rovná ploche náramku:
teda
πr2= 4/3 πr3
⇒ r = 3/4
Polomer náramku je teda 3/4 jednotiek.
Príklad 4: Je dané, že výška sklonu pravého kruhového kužeľa je 25 cm a jeho výška je 24 cm. Nájsť zakrivenú plochu povrchu kužeľa?
java 8
Riešenie:
Vzorec pre zakrivený povrch kužeľa je πrl. Kde r je polomer kužeľa a l je výška sklonu kužeľa.
Tu je kužeľ Pravý kruhový kužeľ.
Polomer kužeľa by teda bol:
r= sqrt{l^2 – h^2}
=>r = sqrt{25^2 – 24^2}
=> r = 7 cm.
Teraz vypočítame zakrivený povrch:
Požadovaná plocha = (22/7) * 7 * 25 = 550 cm2
Zakrivená plocha kužeľa je teda 550 cm 2 .
Príklad 5: Nájdite plochu bočného povrchu valca s polomerom základne 6 palcov a výškou 14 palcov.
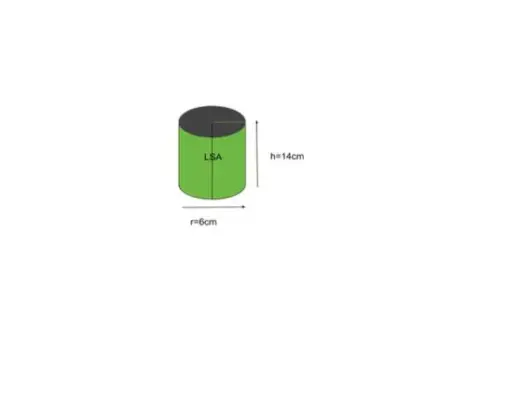
Riešenie:
Daný polomer r = 6, výška h = 14
LSA = 2 rh
= 2 * ∏ * 6 * 14
= 168°
= 527 787
= 528.
LSA daného valca je 528 cm .
Cvičná otázka o povrchových plochách a objemoch
Rôzne Cvičné otázky týkajúce sa plôch a objemu vzorce sú:
Q1. Nájdite povrch kocky s dĺžkou strany 5 centimetrov.
Q2. Vypočítajte objem gule s polomerom 3 metre.
Q3. Určte celkový povrch valca s polomerom 4 centimetre a výškou 8 centimetrov.
Q4. Nájdite objem kužeľa s polomerom 6 palcov a výškou 10 palcov.
Q5. Vypočítajte povrch obdĺžnikového hranola s dĺžkou 7 metrov, šírkou 4 metre a výškou 6 metrov.
Časté otázky o vzorcoch plochy a objemu
Aké sú vzorce pre povrch a objem?
Vo vyššie uvedenom článku sú pridané rôzne vzorce pre plochu a objem.
Aký je vzorec pre objemovú plochu povrchu triedy 10?
Vzorec pre povrchovú a objemovú triedu 10 obsahuje:
| Názov tvaru | Zakrivená plocha povrchu | Celková plocha povrchu | Objem |
|---|---|---|---|
| Kváder selénový tutoriál java | 2 h (l + b) | 2 (lb + bh + hl) | l × b × h |
| Kocka | 4a2 | 6a2 | a3 |
| Valec | 2πrh | 2π(r + h) | πr2h |
| Sphere | 4πr2 | 4πr2 | 4/3π r3 |
| Kužeľ | πrl | πr(r + l) | 1/3π r2h |
| Hemisféra | 2pr2 | 3πr2 | 2/3π r3 |
Aký je vzorec kvádra v oblasti povrchu a objemu?
- Povrch kvádra = 2 (lb + bh + hl)
- Objem kvádra = l × b × h
Čo je povrch a objem?
Plocha povrchu je plocha všetkých povrchov telesa a jej objem je priestor, ktorý zaberá teleso.
