Plocha povrchu hranola: V matematike je hranol základným členom rodiny mnohostenov a je definovaný ako trojrozmerný tvar, ktorý má dva identické mnohouholníky oproti sebe, ktoré sú bočne spojené pravouhlými alebo rovnobežníkovými plochami. Identické mnohouholníky môžu byť trojuholníky, štvorce, obdĺžniky, päťuholníky alebo akýkoľvek iný n-stranný mnohouholník a nazývajú sa základňami hranola. Ostatné strany hranola sú rovnobežníky alebo obdĺžniky.

V tomto článku budeme diskutovať rôzne typy hranolov a povrchová plocha hranolového vzorca s príkladmi a praktickými problémami.

Obsah

• Aký je povrch hranola?
• Rôzne typy hranolov
• Trojuholníkový hranol
• Pravouhlý hranol
• Štvorcový hranol
• Päťuholníkový hranol
• Šesťhranný hranol
• Povrchová plocha hranolového vzorca
• Príklady riešenia povrchu hranola
• Cvičné problémy na povrchu hranola

Aký je povrch hranola?

Plocha povrchu hranola sa označuje ako celková plocha ohraničená všetkými jeho plochami. Aby sme určili povrch hranola, musíme vypočítať plochy každej z jeho plôch a potom pridať výsledné plochy. Hranol má dva druhy povrchových plôch, menovite bočný povrch a celkový povrch. Plocha, ktorú zaberajú strany hranola, s výnimkou dvoch rovnobežných plôch (základne hranola), sa označuje ako jeho bočná plocha.

Bočný povrch hranola = [obvod základne × výška] štvorcové jednotky

Teraz je celkový povrch hranola súčtom plôch jeho dvoch základní a jeho bočnej plochy.

Všeobecný vzorec na výpočet celkovej plochy povrchu akéhokoľvek typu pravého hranola je:

Celková plocha hranola = [2 (plocha základne) + (obvod základne × výška)] štvorcové jednotky

Rôzne typy hranolov

Existujú rôzne typy hranolov na základe tvaru podstavy hranola, ako napr

• Trojuholníkové hranoly,
• Štvorcové hranoly,
• Obdĺžnikové hranoly,
• päťuholníkové hranoly,
• Šesťhranné hranoly,
• Osemhranné hranoly.

Trojuholníkový hranol

Hranol s trojuholníkovou základňou sa označuje ako trojuholníkový hranol. Trojuholníkový hranol pozostáva z troch naklonených pravouhlých plôch a dvoch rovnobežných trojuholníkových podstavcov. Nech H je výška trojuholníkového hranola; a, b a c sú dĺžky strán a h je výška trojuholníkových základní.

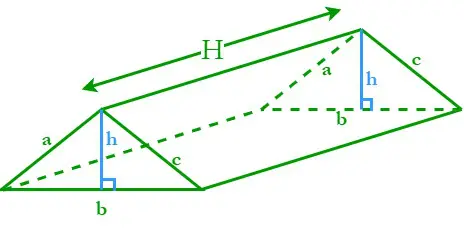
Obvod trojuholníkovej základne (P) = súčet jej troch strán = a + b + c

Plocha trojuholníkovej základne (A) = ½ × základňa × výška = ½ bh

Vieme, že všeobecný vzorec pre bočný povrch pravého hranola je L. S. A. = PH, kde P je obvod základne a A je základná plocha.

Dosadením všetkých hodnôt vo všeobecnom vzorci dostaneme ,

Bočný povrch trojuholníkového hranola = (a + b +c)H štvorcových jednotiek

kde,

a, b, c sú strany trojuholníkovej základne

H je výška trojuholníkového hranola

Vieme, že všeobecný vzorec pre celkový povrch pravého hranola je T. S. A. = PH+2A, kde P je obvod základne, A je základná plocha a H je výška hranola.

Dosadením všetkých hodnôt vo všeobecnom vzorci dostaneme

Celková plocha trojuholníkového hranola = (a + b + c)H + 2 × (½ bh)

Celková plocha trojuholníkového hranola = (a + b + c)H + bh štvorcové jednotky

kde,

a, b, c sú strany trojuholníkovej základne

H je výška trojuholníkového hranola

h je výška trojuholníka

Pravouhlý hranol

Hranol s pravouhlou základňou sa označuje ako pravouhlý hranol. Obdĺžnikový hranol pozostáva zo štyroch pravouhlých plôch a dvoch rovnobežných pravouhlých podstavcov. Nech je výška hranola h a dĺžka a šírka jeho pravouhlých podstav l a w .

Obvod obdĺžnikovej základne (P) = súčet jej štyroch strán = 2 (d + w)

Plocha obdĺžnikovej základne (A) = dĺžka × šírka = l × š

Vieme, že všeobecný vzorec pre bočný povrch pravého hranola je L. S. A. = PH, kde P je obvod základne a A je základná plocha.

Dosadením všetkých hodnôt vo všeobecnom vzorci dostaneme ,

Bočný povrch pravouhlého hranola = 2h(l + w) štvorcových jednotiek

kde,

l je dĺžka

w je šírka

h je výška

Vieme, že všeobecný vzorec pre celkový povrch pravého hranola je T.S.A. = PH+2A, kde P je obvod základne, A je základná plocha a H je výška hranola.

Dosadením všetkých hodnôt vo všeobecnom vzorci dostaneme

Celková plocha pravouhlého hranola = 2h (d + w) + 2 (d × w)

= 2 lh + 2 wh + 2 lw

Celková plocha pravouhlého hranola = 2 (lh + wh + lw) štvorcové jednotky

kde,

l je dĺžka

w je šírka

h je výška

Štvorcový hranol

Hranol so štvorcovou základňou sa označuje ako štvorcový hranol. Štvorcový hranol pozostáva zo štyroch pravouhlých plôch a dvoch rovnobežných štvorcových podstav. Nech je výška hranola h a dĺžka jeho štvorcových podstav je s.

Obvod štvorcovej základne (P) = súčet jej štyroch strán = s + s + s + s = 4 s

Plocha štvorcovej základne (A) = (dĺžka strany)²= s²

Vieme, že všeobecný vzorec pre bočný povrch pravého hranola je L. S. A. = PH, kde P je obvod základne a A je základná plocha.

Nahradením všetkých hodnôt vo všeobecnom vzorci dostaneme,

abeceda v číslach

Bočný povrch štvorcového hranola = 4š štvorcových jednotiek

kde,

s je strana štvorcovej základne

h je výška štvorcového hranola

Vieme, že všeobecný vzorec pre celkový povrch pravého hranola je T.S.A. = PH+2A, kde P je obvod základne, A je základná plocha a H je výška hranola.

Dosadením všetkých hodnôt vo všeobecnom vzorci dostaneme

Celková plocha štvorcového hranola = [4sh + 2s ² ] štvorcových jednotiek

kde,

s je strana štvorcovej základne

h je výška štvorcového hranola

Päťuholníkový hranol

Hranol s päťuholníkovou základňou sa označuje ako päťuholníkový hranol. Päťuholníkový hranol pozostáva z piatich naklonených pravouhlých plôch a dvoch rovnobežných päťuholníkových podstav. Nech h je výška päťuholníkového hranola; a a b sú dĺžka apotémy a dĺžky strán päťuholníkových základní.

Obvod základne päťuholníka (P) = súčet jej piatich strán = 5b

Plocha základne päťuholníka (A) = 5/2 x (dĺžka apotémy) x (dĺžka strany) = 5ab

Vieme, že všeobecný vzorec pre bočný povrch pravého hranola je L. S. A. = PH, kde P je obvod základne a A je základná plocha.

Nahradením všetkých hodnôt vo všeobecnom vzorci dostaneme,

Bočný povrch päťuholníkového hranola = 5bh štvorcových jednotiek

kde,

b je strana päťuholníkovej základne

h je výška päťuholníkového hranola

Vieme, že všeobecný vzorec pre celkový povrch pravého hranola je T.S.A. = PH+2A, kde P je obvod základne, A je základná plocha a H je výška hranola.

Nahradením všetkých hodnôt vo všeobecnom vzorci dostaneme,

Celková plocha päťuholníkového hranola = [5bh + 5ab] štvorcových jednotiek

kde,

b je strana päťuholníkovej základne

a je dĺžka apotémy.

h je výška päťuholníkového hranola

Šesťhranný hranol

Hranol so šesťhrannou základňou sa označuje ako šesťhranný hranol. Šesťhranný hranol pozostáva zo šiestich naklonených pravouhlých plôch a dvoch paralelných šesťhranných podstavcov. Nech h je výška šesťhranného hranola; a sú dĺžky strán šesťuholníkových základní.

Obvod šesťuholníkovej základne (P) = súčet jej šiestich strán = 6a

Plocha základne šesťuholníka (A) = 6 x (plocha rovnostranného trojuholníka)

A = 6 x (√3a²/4) ⇒ A = 3√3a²/2

Vieme, že všeobecný vzorec pre bočný povrch pravého hranola je L. S. A. = PH, kde P je obvod základne a A je základná plocha.

Nahradením všetkých hodnôt vo všeobecnom vzorci dostaneme,

Bočný povrch šesťhranného hranola = 6ah štvorcových jednotiek

kde,

a je strana šesťuholníkovej základne

h je výška šesťuholníkovej základne

Vieme, že všeobecný vzorec pre celkový povrch pravého hranola je T.S.A. = PH+2A, kde P je obvod základne, A je základná plocha a H je výška hranola.

Dosadením všetkých hodnôt vo všeobecnom vzorci dostaneme

Celková plocha šesťhranného hranola = [6ah +3√3a²] štvorcových jednotiek

kde,

a je strana šesťuholníkovej základne

h je výška šesťhrannej základne:

Povrchová plocha hranolového vzorca

Nižšie uvedená tabuľka poskytuje vzorec pre rôzne typy hranolov:

Príklady riešenia povrchu hranola

Úloha 1: Aká je výška hranola, ktorého základná plocha je 36 štvorcových jednotiek, obvod základne je 24 jednotiek a jej celková plocha je 320 štvorcových jednotiek?

Riešenie:

Vzhľadom na údaje,

Základná plocha = 36 štvorcových jednotiek

Obvod základne = 24 jednotiek

Celková plocha hranola = 320 štvorcových jednotiek

Máme,

Celková plocha hranola = (2 × plocha základne) + (obvod základne × výška)

⇒ 320 = (2 × 36)+ (24 × h)

⇒ 24h = 248 ⇒ h = 10,34 jednotiek

Výška daného hranola je teda 10,34 jednotiek.

Úloha 2: Nájdite celkový povrch štvorcového hranola, ak je výška hranola 13 cm a dĺžka strany štvorcovej základne 4 cm.

Riešenie:

Vzhľadom na údaje,

Výška štvorcového hranola (v) = 13 cm

Dĺžka strany štvorcovej základne (a) = 4 cm

My to vieme,

Celková plocha štvorcového hranola = 2a²+ 4 hodiny

= 2 × (4)²+ 4 × 4 × 13

= 32 + 208 = 240 cm²

Celková plocha daného hranola je teda 240 cm2.

Úloha 3: Určte základnú dĺžku päťuholníkového hranola, ak jeho celková plocha je 100 štvorcových jednotiek a jeho výška je 8 jednotiek a dĺžka apotému je 5 jednotiek.

Riešenie:

Vzhľadom na údaje,

Celková plocha päťuholníkového hranola = 100 štvorcových jednotiek

Výška hranola (h) = 8 jednotiek

Dĺžka apotému (a) = 5 jednotiek

My to vieme,

Celková plocha päťbokého hranola = 5ab + 5bh

⇒ 100 = 5b (a+ h)

⇒ 100/5 = b (5 + 8)

⇒ 20 = b × (13) ⇒ b = 25/16 = 1,54 jednotiek

Preto je základná dĺžka 1,54 jednotiek

Problém 4: Určte výšku pravouhlého hranola a celkovú plochu pravouhlého hranola, ak jeho bočná plocha je 540 cm2 a dĺžka a šírka základne je 13 cm a 7 cm.

Riešenie:

Vzhľadom na údaje,

Dĺžka obdĺžnikovej základne (l) = 13 cm

Šírka obdĺžnikovej základne (š) = 7 cm

Bočný povrch hranola = 540 cm2

Máme,

Bočný povrch hranola = obvod základne × výška

⇒ 540 = 2 (d + š) h

⇒ 2 (13 + 7) h = 540

⇒ 2 (20) v = 540 ⇒ v = 13,5 cm

My to vieme,

Celková plocha pravouhlého hranola = 2 (lw + wh + lh)

= 2 × (13 × 7 + 7 × (13,5) + 13 × (13,5))

disketa

= 2 × (91 + 94,5 + 175,5) = 722 cm2

Výška a celková plocha daného pravouhlého hranola sú teda 13,5 cm a 722 cm2.

Úloha 5: Určte povrchovú plochu pravidelného šesťhranného hranola, ak je výška hranola 12 palcov a dĺžka strany základne je 5 palcov.

Riešenie:

Vzhľadom na údaje,

Výška hranola (h) = 12 palcov

Dĺžka strany základne (a) = 6 palcov

Povrch pravidelného šesťhranného hranola = 6ah + 3√3a²

= 6 × 5 × 12 + 3√3(5)²

= 360 + 75√3

= 360 + 75 × (1,732) = 489,9 štvorcových palcov

Plocha povrchu daného hranola je teda 489,9 palcov štvorcových.

Úloha 6: Vypočítajte bočné a celkové povrchy trojuholníkového hranola, ktorého obvod základne je 25 palcov, dĺžka základne a výška trojuholníka sú 9 palcov a 10 palcov a výška hranola je 14 palcov.

Riešenie:

Vzhľadom na údaje,

Výška hranola (H) = 14 palcov

Základný obvod hranola (P) = 25 palcov

Základná dĺžka trojuholníka = 9 palcov

Výška trojuholníka = 10 palcov

My to vieme,

Bočný povrch hranola = obvod základne × výška

= 25 × 14 = 350 štvorcových palcov

Plocha trojuholníkovej základne (A) = ½ × základňa × výška = 1/2 × 9 × 10 = 45 štvorcových palcov

Celková plocha trojuholníkového hranola = 2A + PH

= 2 × 45 + 25 × 14 = 90 + 350 = 440 štvorcových palcov

Bočná a celková plocha hranola je teda 350 štvorcových palcov a 440 štvorcových palcov.

Cvičné problémy na povrchu hranola

1. Daný obdĺžnikový hranol s rozmermi:

• Dĺžka = 6 cm
• Šírka = 4 cm
• Výška = 5 cm

Vypočítajte celkový povrch.

2. Uvažujme trojuholníkový hranol s rozmermi:

• Základňa trojuholníka = 8 cm
• Výška trojuholníka = 6 cm
• Dĺžka hranola = 10 cm

Nájdite celkovú plochu povrchu.

3. Určte povrch pravidelného päťuholníkového hranolu pomocou:

• Dĺžka strany základne = 7 cm
• Výška hranola = 9 cm.

4. Vypočítajte povrch šesťhranného hranolu pomocou:

• Dĺžka strany pravidelnej šesťhrannej základne = 10 cm
• Výška hranola = 12 cm.

Povrchová plocha hranola – často kladené otázky

Čo je hranol v geometrii?

Hranol je trojrozmerný tvar s dvoma zhodnými rovnobežnými základňami a pravouhlými alebo rovnobežníkovými bočnými stenami, ktoré ich spájajú. Hranoly sa dodávajú v rôznych formách, ako sú pravouhlé hranoly, trojuholníkové hranoly a päťuholníkové hranoly, pričom každý má jedinečné vlastnosti.

Ako zistíte povrchovú plochu hranola?

Ak chcete nájsť povrchovú plochu hranola, vypočítajte plochy všetkých jeho plôch a potom ich spočítajte. Pre pravouhlý hranol je vzorec plochy povrchu 2lw + 2lh + 2wh, kde l je dĺžka, w je šírka a h je výška. Pre iné typy hranolov, ako sú trojuholníkové alebo päťuholníkové hranoly, môžu byť potrebné ďalšie vzorce pre základnú plochu a bočnú plochu.

Aké sú vlastnosti hranola?

Hranoly majú niekoľko kľúčových vlastností:

• Majú dve zhodné paralelné základne.
• Všetky bočné strany sú rovnobežníky.
• Nadmorská výška (výška) je kolmá vzdialenosť medzi dvoma základňami.
• Základy majú rovnaký tvar a veľkosť.
• Priečny rez rovnobežný so základňami má vždy rovnaký tvar a veľkosť ako základne.

Aké sú niektoré príklady hranolov v reálnom živote?

Hranoly možno nájsť v rôznych každodenných predmetoch a štruktúrach. Príklady:

• Obdĺžnikové hranoly: Budovy, krabice na obilniny, knihy.
• Trojuholníkové hranoly: Strechy domov, klinovité objekty.
• Päťuholníkové hranoly: Niektoré typy stĺpov, určité architektonické štruktúry.
• Šesťhranné hranoly: Určité typy kryštálov, niektoré obalové nádoby.

Prečo je povrchová plocha pri hranoloch dôležitá?

Plocha povrchu je pri hranoloch rozhodujúca, pretože predstavuje celkovú plochu všetkých plôch (čiel) hranola. Pochopenie plochy povrchu pomáha pri rôznych praktických aplikáciách, ako je výpočet množstva materiálu potrebného na stavbu alebo zakrytie objektu v tvare hranola, určenie rýchlosti prenosu tepla a optimalizácia dizajnu obalu.