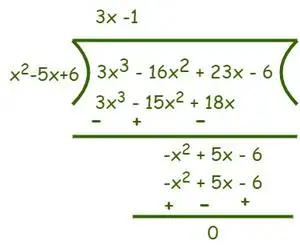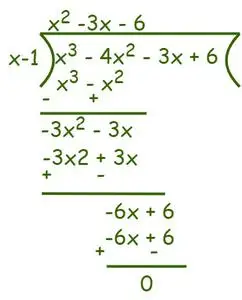Kubická rovnica je matematická rovnica, v ktorej sa polynóm 3. stupňa rovná konštante alebo inému polynómu maximálneho 2. stupňa. Štandardné znázornenie kubickej rovnice je sekera ³ +bx ² +cx+d = 0 kde a, b, c a d sú reálne čísla. Niektoré príklady kubickej rovnice sú X ³ – 4x ² + 15x – 9 = 0, 2x ³ – 4x ² = 0 atď.

Obsah

• Definícia polynómu
• Stupeň rovnice
• Definícia kubickej rovnice
• Ako riešiť kubické rovnice?
• Riešenie kubických rovníc
• Riešenie kubickej rovnice pomocou faktorov
• Riešenie kubickej rovnice pomocou grafickej metódy
• Problémy založené na riešení kubických rovníc
• Cvičenie úloh pri riešení kubických rovníc

Aby sme sa naučili ako riešiť kubické rovnice, musíme sa najprv naučiť o polynómoch, stupni polynómu a iných. V tomto článku sa podrobne dozvieme o polynómoch, polynomických rovniciach, riešení kubických rovníc alebo ako riešiť kubické rovnice a ďalších.

Definícia polynómu

Polynóm je definovaný takto:

A polynóm je algebraický výraz, v ktorom mocninou premennej je nezáporné celé číslo. Všeobecný tvar polynómu je a₀Xⁿ+ a₁X^n-1+ a₂X^n-2+… + a_n. V závislosti od maximálnej sily premennej možno polynóm klasifikovať ako monomický, binomický, trojčlenný atď.

Čo je to rovnica?

Rovnica je definovaná takto,

Rovnica je polynóm, ktorý sa rovná číselnej hodnote alebo akémukoľvek inému polynómu. Napríklad x + 2 je polynóm, ale x + 2 = 5 je rovnica. Podobne 2x + 3 = x + 1 je tiež rovnica, zatiaľ čo 2x + 3 a x + 1 sú polynómy jednotlivo.

Stupeň rovnice

Definícia stupňa rovnice je uvedená nižšie:

Stupeň rovnice je definovaný ako maximálny výkon, ktorý má premenná v rovnici.

Na základe stupňa rovnice možno rovnicu klasifikovať takto:

• Lineárna rovnica
• Kvadratická rovnica
• Kubická rovnica
• Bikvadratická rovnica

Lineárna rovnica

Rovnica, v ktorej je maximálna mocnina premennej 1, sa nazýva lineárna rovnica.

• Napríklad 3x +1 = 0

Kvadratický polynóm

Rovnica, v ktorej je maximálna mocnina premennej 2, je kvadratická rovnica.

• Napríklad 3x²+x+1 = 0

Kubická rovnica

Rovnica, v ktorej je maximálna mocnina premennej 3, sa nazýva kubická rovnica.

• Napríklad 5x³+3x²+x+1 = 0

Bikvadratický polynóm

Rovnica, v ktorej je maximálna mocnina premennej 4, sa nazýva bikvadratický polynóm alebo kvartický polynóm.

ako previesť celé číslo na reťazec v jave

• Napríklad 5x⁴+4x³+3x²+2x+1 = 0

Definícia kubickej rovnice

Kubická rovnica je algebraická rovnica, kde najvyšší stupeň polynómu je 3. Niektoré príklady kubických rovníc sú 5x³+3x²+x+1 = 0, 2x³+8 = x ⇒ 2x³-x+8 = 0 atď.

Všeobecný tvar kubickej rovnice je,

sekera ³ + bx ² + cx + d = 0, a ≠ 0

Kde,

• a, b, a c sú koeficienty premennej a ich exponáty a d je konštanta a
• a, b, c a d sú reálne čísla.

Ako riešiť kubické rovnice?

Kubická rovnica je rovnica s tretím stupňom. Má tri riešenia a dá sa ľahko vyriešiť podľa krokov pridaných nižšie,

Krok 1: Nájdite jedno riešenie kubickej rovnice metódou hit a skúste. Predpokladajme, že máme kubickú rovnicu P(x), potom nájdite pre ľubovoľné x = a, P(a) = 0 tak, že vezmeme, x = 0, ±1, ±2, ±3, … atď.

Krok 2: Keď dostaneme, P(a) = 0, nájdite faktor (x – a) P(x)

Krok 3: Vydeľte P(x) (x – a), aby ste dostali kvadratickú rovnicu, povedzme Q(x) pomocou delenia polynómom.

Krok 4: Faktarizujte kvadratickú rovnicu Q(x), aby ste dostali faktory ako (x – b) a (x – c).

Krok 5: (x – a), (x – b) a (x – c) sú faktory P(x) a riešením každého faktora dostaneme korene rovnice ako, a, b a c.

Naučiť sa viac o, Deliaci polynóm

Riešenie kubických rovníc

A Kubická rovnica možno vyriešiť dvoma spôsobmi

• Redukovaním na kvadratickú rovnicu a jej riešením buď faktorizáciou alebo kvadratickým vzorcom
• Grafickou metódou

A Kubická rovnica má tri korene. Tieto korene môžu byť skutočné alebo imaginárne. Tiež môžu existovať odlišné korene alebo dva rovnaké a jeden odlišný koreň a všetky tri rovnaké korene.

Treba poznamenať, že pre akúkoľvek rovnicu vrátane Kubické rovnice , rovnica musí byť vždy pred riešením rovnice najprv usporiadaná v jej štandardnom tvare.

Napríklad, ak je daná rovnica 2x²-5 = x + 4/x, potom to musíme znova usporiadať do štandardného tvaru, t.j. 2x³-X²-5x-4 = 0. Teraz môžeme rovnicu vyriešiť pomocou akejkoľvek vhodnej metódy.

Riešenie kubickej rovnice pomocou faktorov

Riešenie kubickej rovnice pomocou faktorovej vety je vysvetlené pomocou príkladu pridaného nižšie,

Príklad: Nájdite korene rovnice f(x) = 3x ³ -16x ² + 23x − 6 = 0.

Riešenie:

Daný výraz: f(x) = 3x³-16x²+ 23x − 6 = 0

Najprv rozložte polynóm na faktor, aby ste získali korene

Keďže konštanta je -6, možné faktory sú 1, 2, 3, 6

f(1) = 3 – 16 + 23 – 6 ≠ 0

f(2) = 24 – 64 + 46 – 6 = 0

f(3) = 81 – 144 + 69 – 6 = 0

f(6) = 648 – 576 + 138 – 6 ≠ 0

Podľa toho to vieme Faktorová teoréma ak f(a) = 0, potom (x-a) je faktor f(x)

Takže (x – 2) a (x – 3) sú faktory f(x). Preto súčin (x – 2) a (x – 3) bude tiež faktorom f(x). Teraz na nájdenie zostávajúcich faktorov použite metódu dlhého delenia a vydeľte f(x) súčinom (x – 2) a (x – 3)

Deliteľ = (x – 2) (x – 3) = (x²– 5x + 6) a dividenda = 3x³-16x²+ 23x − 6. Teraz rozdeľte, ako je znázornené nižšie,

Po delení dostaneme (3x-1) ako kvocient a zvyšok je 0. Teraz ako na Algoritmus delenia my to vieme Dividenda = Deliteľ × Podiel + Zostatok.

⇒ f(x) = (3x³-16x²+ 23x − 6) = (x²– 5x + 6) (3x-1)

Pretože f(x) = 0

⇒ (x²– 5x + 6)(3x-1) = 0

⇒ x²– 5x + 6 = 0 alebo 3x-1 = 0

Teraz vezmeme 3x-1 = 0 ⇒ x = 1/3, pretože už poznáme dva korene z x²– 5x + 6, čo sú 2 a 3

takže,

Korene daného Kubická rovnica sú 1/3, 2 a 3.

Riešenie kubickej rovnice pomocou grafickej metódy

Kubická rovnica je vyriešená graficky, keď nemôžete vyriešiť danú rovnicu pomocou iných techník. Potrebujeme teda presné nakreslenie danej kubickej rovnice. Korene rovnice sú body, v ktorých graf pretína os X, ak je rovnica v členoch x a ak je rovnica v členoch y, potom korene rovnice sú body, v ktorých je graf odreže os Y.

Počet reálnych riešení kubickej rovnice sa rovná počtu, koľkokrát graf kubickej rovnice pretne os X.

Príklad: Nájdite korene rovnice f(x) = x ³ - 4x ² − 9x + 36 = 0 pomocou grafickej metódy.

Riešenie:

Daný výraz: f(x) = x³- 4x²− 9x + 36 = 0.

Teraz jednoducho nahraďte náhodné hodnoty za x v grafe pre danú funkciu:

X	-4	-3	-2	-1	0	1	2	3	4	5
f(x)	-56	0	19	40	36	24	10	0	0	16 napíšte json do súboru python

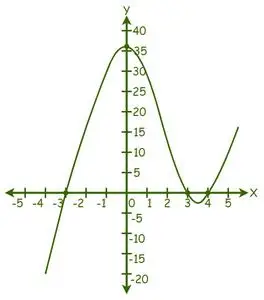
Vidíme, že graf preťal os X v 3 bodoch, preto existujú 3 reálne riešenia.

Riešenia z grafu sú: x = -3, x = 3 a x = 4.

Korene danej rovnice sú teda -3, 3 a 4.

Čítaj viac,

• Lineárna rovnica
• Riešenie kvadratickej rovnice
• Faktorizácia polynómov

Problémy založené na riešení kubických rovníc

Úloha 1: Nájdite korene f(x) = x ³ – 4x ² -3x + 6 = 0.

Riešenie:

Daný výraz: f(x) = x³– 4x²-3x + 6 = 0.

Najprv rozložte polynóm na faktor, aby ste získali korene.

Keďže konštanta je +6, možné faktory sú 1, 2, 3, 6.

f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0

f(2) = 8 – 16 – 6 + 6 ≠ 0

f(3) = 27 – 36 – 9 + 6 ≠ 0

f(6) = 216 – 144 -18 + 6 = -48 ≠ 0

Takže podľa Faktorová teoréma (x – 1) je faktor danej rovnice. Teraz na nájdenie zostávajúcich faktorov použite metódu dlhého delenia.

Podľa Algoritmus delenia môžeme písať,

Takže f(x) = x³– 4x²-3x + 6 = (x – 1) (x²– 3x – 6) = 0

⇒ (x – 1) = 0 alebo (x²– 3x – 6) = 0

Vieme, že korene kvadratickej rovnice sú os²+ bx + c = 0 je,

x = [-b ± √(b²-4ac)]/2a

Preto pre (x²– 3x – 6) = 0

x = [3 ± √(3²– 4(1)(-6)]/2(1)

x = (3 ± √33)/2

Korene danej kubickej rovnice sú teda 1, (3+√33)/2 a (3–√33)/2.

Úloha 2: Nájdite korene rovnice f(x) = 4x ³ – 10x ² + 4x = 0.

Riešenie:

Daný výraz: f(x) = 4x³– 10x²+ 4x = 0

⇒ x (4x²– 10x + 4) = 0

⇒ x (4x²– 8x – 2x + 4) = 0

⇒ x(4x(x – 2) – 2(x – 2)) = 0

⇒ x (4x – 2) (x – 2) = 0

⇒ x = 0 alebo 4x – 2 = 0, x – 2 = 0

⇒ x = 0 alebo x = 1/2 alebo x = 2

trieda vs objekt v jave

Korene danej rovnice sú teda 0, 1/2 a 2.

Úloha 3: Nájdite korene rovnice f(x) = x ³ + 3x ² + x + 3 = 0.

Riešenie:

Daný výraz: f(x) = x³+ 3x²+ x + 3 = 0.

⇒ x²(x + 3) + 1 (x + 3) = 0

⇒ (x + 3) (x²+1) = 0

⇒ x + 3 = 0 alebo x²+1 = 0

⇒ x = -3, ±i

Daná rovnica má teda reálny koreň, t.j. -3, a dva imaginárne korene, t.j. ±i.

Úloha 4: Nájdite korene rovnice f(x) = x ³ – 7x ² – x + 7 = 0.

Riešenie:

Dané výrazy,

f(x) = x³– 3x²– 5x + 7 = 0

Najprv rozlož rovnicu, f(x): x³– 3x²– 5x + 7 = 0

Dá sa rozdeliť na (x-7)(x+1)(x-1) = 0

Po faktorizácii polynómu môžeme nájsť korene tak, že každý faktor prirovnáme k nule. Napríklad:

• x – 7 = 0, teda x = 7
• x + 1 = 0, teda x = -1
• x – 1 = 0, teda x = 1

Takže korene rovnice f(x): x³– 3x²– 5x + 7 = 0 árov

• x = 7
• x = -1
• x = 1

Úloha 5: Nájdite korene rovnice f(x) = x ³ - 6x ² + 11x − 6 = 0 pomocou grafickej metódy.

Riešenie:

Daný výraz: f(x) = x³- 6x²+ 11x − 6 = 0.

Teraz jednoducho nahraďte náhodné hodnoty za x v grafe pre danú funkciu:

X	1	2	3	4	5
f(x)	0	0	0	6	24 skúste catch block v jave

Vidíme, že graf preťal os X v 3 bodoch, preto existujú 3 reálne riešenia.

Riešenia z grafu sú: x = 1, x = 2 a x = 3.

Korene danej rovnice sú teda 1, 2 a 3.

Cvičenie úloh pri riešení kubických rovníc

Rôzne praktické problémy súvisiace s kubickými rovnicami sú pridané nižšie. Vyriešte tieto problémy, aby ste plne pochopili koncept Ako vyriešiť kubickú rovnicu?

P1. Vyriešte kubickú rovnicu, 3x³+ 2x²– 11x + 7 = 0.

P2. Nájdite korene kubickej rovnice, 4x³– 12x²+ 17 = 0.

P3. Vyriešte kubickú rovnicu, x³+ 4x²– x + 3 = 0 pomocou grafickej metódy.

P4. Nájdite číslo, ktoré vyhovuje, -9x³+ 11x²– 8x + 2 = 0.

Často kladené otázky o riešení kubických rovníc

1. Čo sú to kubické rovnice?

Kubické rovnice sú algebraické rovnice, v ktorých maximálna mocnina premennej je 3

2. Ako vynásobíte kubickú rovnicu?

Kubickú rovnicu môžeme faktorizovať dvoma spôsobmi. Najprv získaním lineárneho výrazu spoločného z danej kubickej rovnice potom získame lineárny a kvadratický výraz ako súčin. Túto kvadratickú rovnicu možno ďalej faktorizovať, aby sme získali všetky faktory. Druhou metódou je nájsť nulu danej kubickej rovnice zadaním náhodných hodnôt. Hodnota, pre ktorú dostaneme hodnotu rovnice nulovú, bude jednou z núl danej kubickej rovnice. Teraz pomocou faktorovej vety vytvorte lineárny výraz, povedzme x-a a vydeľte danú kubickú rovnicu týmto výrazom, čím získate kvadratickú rovnicu ako kvocient. Táto získaná kvadratická rovnica môže byť ďalej faktorizovaná, aby sa získali všetky faktory.

3. Ako graficky vyriešite kubickú rovnicu?

Na vyriešenie kubickej rovnice graficky vložte náhodné hodnoty pre x do danej kubickej rovnice a vyriešite, dostanete hodnoty y. Tieto získané hodnoty vyneste do grafu. Nájdite súradnice, v ktorých graf pretína os x. Tieto súradnice sú riešením kubickej rovnice.

4. Môžu byť všetky kubické rovnice presne vyriešené?

Každá rovnica, ktorá má nepárnu mocninu, musí mať jeden skutočný koreň. Kubická rovnica teda musí mať aspoň jeden skutočný koreň, na rozdiel od kvadratickej rovnice, kde oba korene môžu byť imaginárne, keď je diskriminant menší ako nula.

5. Môže mať kubická rovnica viacero riešení?

Áno, kubické rovnice môžu mať viacero riešení, keďže kubická rovnica môže mať až tri odlišné skutočné korene.

6. Čo rozumiete pod pojmom stupeň rovnice?

Maximálny výkon, ktorý má premenná v rovnici, sa nazýva stupeň polynómu.

7. Aký je rozdiel medzi polynómom a rovnicou?

Polynóm je jednoducho algebraická rovnica, v ktorej mocnina premennej je nezáporné celé číslo. Tento polynóm, keď sa porovnáva (=) s číselnou hodnotou alebo iným polynómom, sa nazýva rovnica.

8. Čo je to faktorová veta pre kubické rovnice?

Faktorová teoréma hovorí, že ak r je koreň (riešenie) kubickej rovnice ax³+ bx²+ cx + d = 0, potom x – r je faktor rovnice.

9. Čo ak nemôžem nájsť presné riešenia pomocou vzorcov?

Ak sa nám zdá nemožné nájsť presné riešenia, môžeme použiť numerické metódy, ako sú iteračné metódy (napr. Newtonova metóda) na aproximáciu koreňov rovnice.

Naučiť sa viac o Newton Raphsonova metóda .