Vzorec sklonu sa používa na určenie strmosti alebo sklonu čiary. Súradnice x a y bodov ležiacich na priamke sa používajú na výpočet sklonu priamky. Zmena súradnice y súvisiaca so zmenou súradníc x sa nazýva sklon priamky a zvyčajne sa označuje písmenom m.

Obsah

• Čo je Slope Formula?
• Svahový vzorec
• Odvodenie sklonového vzorca
• Vzorec sklonu priamky (priamka).
• Sklonová rovnica
• Príklad na Slope Formule

Čo je Slope Formula?

Na výpočet sklonu čiary je potrebný vzorec sklonu. Na výpočet sklonu priamky sú potrebné súradnice x a y bodov na priamke. Pomer zmeny súradníc y a zmeny súradníc x sa nazýva sklon priamky.

Sklon (m) = zmena y/zmena x = Δy/Δx

Svahový vzorec

V matematike sa sklon čiary používa na určenie toho, ako veľmi sa čiara naklonila, t. j. strmosť čiary. Na určenie sklonu priamky potrebujeme súradnice x a y bodov ležiacich na priamke. Vzorec sklonu je čistá zmena súradnice y vydelená čistou zmenou súradnice x. Δy je zmena súradníc y a Δx je zmena súradníc x. Pomer zmeny súradníc y vzhľadom na zmenu súradníc x je teda daný vzťahom:

Sklon (m) = zmena y/zmena x = Δy/Δx

m= (a ₂ - a ₁ )/(X ₂ - X ₁ )

kde

• X₁a x₂sú súradnice osi X
• a₁a y₂sú súradnice osi Y

Odvodenie sklonového vzorca

Súradnice x a y čiary sa používajú na výpočet sklonu čiary. Čistá zmena súradnice y je Δy, zatiaľ čo čistá zmena súradnice x je Δx. Takže zmenu súradnice y vzhľadom na zmenu súradnice x možno zapísať ako,

m = Δy/Δx

kde,

• m je sklon
• Δy je zmena y-ových súradníc
• Δx je zmena x-ových súradníc

Vieme, že tan θ je tiež sklon priamky, kde θ je uhol vytvorený priamkou s kladným smerom osi x.

a tan θ = výška/základňa

Keďže výška/základňa medzi ľubovoľnými dvomi danými bodmi = (y₂- a₁)/(X₂- X₁)

Rovnica sklonu teda je, m = tan θ = Δy/Δx

Z grafu vidíme:

fronta priority java

Δy = (y₂- a₁)

Δx = (x₂- X₁)

Potom je vzorec sklonu daný ako:

Sklon = m = (y ₂ - a ₁ )/(X ₂ - X ₁ )

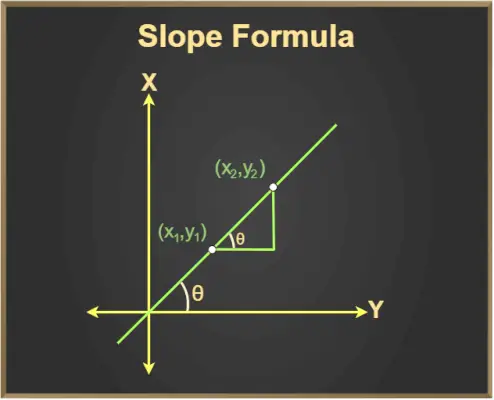
Vzorec sklonu priamky (priamka).

• My to vieme tan θ je tiež sklon čiary, preto sklon čiary môže byť reprezentovaný aj ako,

Sklon (m) = tan θ = Δy/Δx

Kde i je uhol, ktorý zviera priamka w.r.t s kladnou osou X,

trieda java string

• Δy = zmena súradníc y,
• Δx = zmena súradníc x.

• Sklon čiary môžeme definovať aj ako pomer stúpania vzhľadom na priebeh.

Sklon (m) = stúpanie/beh

• Nech ax + by + c = 0 je všeobecná rovnica priamky. Teraz je vzorec pre sklon čiary daný:

Sklon (m) = – koeficient x / koeficient y = -a/b

• Tvar priesečníka so sklonom čiary pomocou rovnice čiary je daný ako,

y = mx + c

Kde m je sklon priamky a c je priesečník v osi y.

Sklonová rovnica

Vzorec sklonu sa používa na určenie sklonu čiary. Rovnica, ktorá sa používa pri hľadaní sklonu, je napísaná takto:

m = tanθ = Δy/Δx = (y ₂ - a ₁ )/(X ₂ - X ₁ )

kde,

• m je sklon čiary
• Δy je rozdiel v y-ových súradniciach
• Δx je rozdiel v súradniciach x
• i je uhol, ktorý zviera čiara s kladnou osou x

Rovnica priamky so sklonom m je daná vzťahom,

y = mx + c

kde,

• m je sklon čiary
• b je priesečník osi y

Čítaj viac,

• Paralelné čiary
• Formulár na zachytávanie svahov

Príklad na Slope Formule

Príklad 1: Nájdite sklon priamky, ktorej súradnice sú (3, 7) a (5, 8).

Riešenie:

Vzhľadom na to, (x₁, a₁) = (3,7) a (x₂, a₂) = (5,8)

Vzorec sklonu (m) = (y ₂ - a ₁ )/(X ₂ - X ₁ )

⇒ m = (8 – 7)/(5 – 3) = 1/2

Sklon danej čiary je teda 1/2.

Príklad 2: Určte sklon priamky, ktorej súradnice sú (7, -5) a (2, -3).

Riešenie:

Vzhľadom na to, (x₁, a₁) = (7, -5) a (x₂, a₂) = (23)

Vzorec sklonu (m) = (y ₂ - a ₁ )/(X ₂ - X ₁ )

⇒ m = (-3 – (-5))/(2 – 7) = -2/5

Sklon danej čiary je teda -2/5

Príklad 3: Nájdite hodnotu a, ak je sklon priamky prechádzajúcej bodmi (-4, a) a (2, 5) 3.

Riešenie:

Java null check

Vzhľadom na to, (x₁, a₁) = (4,a) a (x₂, a₂) = (2, 5) a sklon (m) = 3

Vieme, že sklon (m) = (y ₂ - a ₁ )/(X ₂ - X ₁ )

⇒ 3 = (5 – a)/(2 – 4)

⇒ 3 = (5 – a)/(-2)

⇒ -6 = 5 – a ⇒ a = 5 + 6 = 11

numpy log

Preto hodnota a = 11

Príklad 4: Ak priamka zviera s kladnou osou Y uhol 60°, aká je potom hodnota sklonu priamky?

Riešenie:

Dané údaje, Uhol vytvorený priamkou s kladnou osou y = 60°

Vieme, že ak priamka zviera s kladnou osou y uhol 60°, tak s osou x zviera uhol (90° – 60° = 30°).

Preto hodnota sklonu čiary (m) = tan 30° = 1/√3

Preto je hodnota sklonu priamky = 1/√3.

Príklad 5: Sheela kontrolovala graf a všimla si, že zvýšenie bolo 12 jednotiek a počet jednotiek bol 4. Teraz vypočítajte sklon čiary.

Riešenie:

Dané údaje, vzostup = 12 jednotiek a beh = 4 jednotky

Vieme, že sklon (m) = stúpanie/beh

⇒ m = 12/4 = 3

Sklon danej čiary je teda 3

Príklad 6: Nájdite sklon priamky 3x – 7y + 8 = 0.

Riešenie:

Dané údaje, rovnica priamky = 3x – 7y + 8 = 0

Teraz porovnajte dané so všeobecnou rovnicou priamky, t.j. ax + by + c = 0

Preto a = 3, b = -7 a c = 8

Vieme, že sklon (m) = – koeficient x/koeficient y = -a/b

reťazec na rozhovor

⇒ m = -3/(-7) = 3/7

Sklon danej čiary je teda 3/7.

Cvičné otázky o svahovom vzorci

Q1. Vypočítajte sklon priamky prechádzajúcej bodmi (2, 3) a (5, 7)

Q2. Vzhľadom na rovnicu priamky: y = 3x – 11, aký je jej sklon?

Q3. Ak je sklon priamky 5/6 a prechádza bodom (2, 5), aká je rovnica priamky v tvare sklonu-priesečník?

Q4. Vypočítajte sklon priamky rovnobežnej s priamkou (0, -3) a (1, 11)

Q5. Ak je sklon priamky nedefinovaný, čo môžete o tejto priamke vyvodiť?

Často kladené otázky o Slope Formule

Aký je sklon čiary?

Sklon priamky je hodnota strmosti alebo sklonu priamky v rovine x-y. Sklon sa vypočíta pomocou rôznych metód v závislosti od toho, či je daná rovnica priamky alebo súradnice bodov na priamke.

Aký je vzorec na nájdenie sklonu tangentového vzorca?

Sklon čiary sa vypočíta pomocou daného vzorca. Predpokladajme, že dané súradnice dvoch bodov ležiacich na priamke sú (x₁, a₁)/(X_2,a₂). Potom je vzorec daný ako, Sklon = m = tan θ = (y ₂ - a ₁ )/(X ₂ - X ₁ )

Aká je definícia vzorca sklonu?

Vzorec sklonu je definovaný ako,

• Sklon = (zmena súradnice y)/(zmena súradnice x)
• Sklon = stúpanie/beh.

Aký je sklon vzorca grafu?

Sklon priamky je mierou jej sklonu s kladnou osou x. Matematicky je sklon definovaný ako povzniesť sa nad beh .