Čo je to zoznam preskočení?
Preskakovací zoznam je pravdepodobnostná dátová štruktúra. Preskakovací zoznam sa používa na uloženie zoradeného zoznamu prvkov alebo údajov s prepojeným zoznamom. Umožňuje efektívne prezeranie procesov prvkov alebo údajov. V jednom jedinom kroku preskočí niekoľko prvkov celého zoznamu, a preto je známy ako zoznam preskočení.
Zoznam preskočení je rozšírenou verziou prepojeného zoznamu. Umožňuje používateľovi veľmi rýchlo vyhľadávať, odstraňovať a vkladať prvok. Pozostáva zo základného zoznamu, ktorý obsahuje množinu prvkov, ktoré udržiavajú hierarchiu odkazov nasledujúcich prvkov.
Preskočiť štruktúru zoznamu
Je postavená v dvoch vrstvách: najnižšia vrstva a vrchná vrstva.
Najnižšia vrstva vynechaného zoznamu je bežný zoradený prepojený zoznam a vrchné vrstvy vynechaného zoznamu sú ako „výrazný riadok“, kde sú prvky preskočené.
Tabuľka zložitosti zoznamu preskočenia
| Áno nie | Zložitosť | Priemerný prípad | V najhoršom prípade |
|---|---|---|---|
| 1. | Zložitosť prístupu | O(logn) | O(n) |
| 2. | Zložitosť vyhľadávania | O(logn) | O(n) |
| 3. | Odstráňte zložitosť | O(logn) | O(n) |
| 4. | Vložte zložitosť | O(logn) | O(n) |
| 5. | Priestorová zložitosť | - | O(nlogn) |
Práca so zoznamom preskočení
Zoberme si príklad, aby sme pochopili fungovanie zoznamu preskočení. V tomto príklade máme 14 uzlov, takže tieto uzly sú rozdelené do dvoch vrstiev, ako je znázornené na obrázku.
Spodná vrstva je spoločná čiara, ktorá spája všetky uzly, a horná vrstva je expresná čiara, ktorá spája iba hlavné uzly, ako môžete vidieť na diagrame.
Predpokladajme, že v tomto príklade chcete nájsť 47. Spustíte vyhľadávanie od prvého uzla expresnej linky a budete pokračovať v jazde na expresnej linke, kým nenájdete uzol, ktorý sa rovná 47 alebo viac ako 47.
V príklade môžete vidieť, že 47 v expresnom riadku neexistuje, takže hľadáte uzol menší ako 47, čo je 40. Teraz prejdete na normálny riadok s pomocou 40 a vyhľadáte 47, ako je znázornené na diagrame.
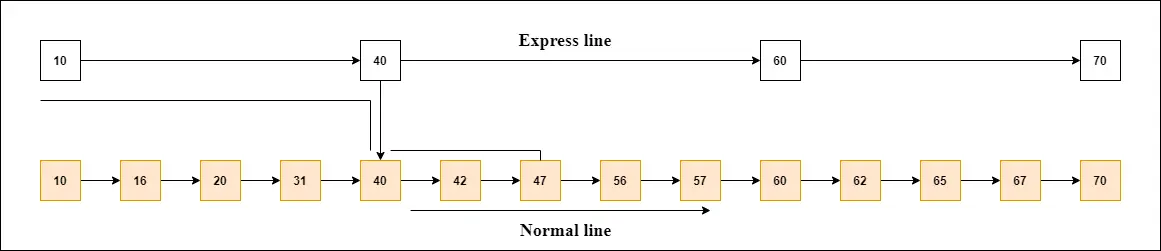
Poznámka: Keď nájdete takýto uzol na 'expresnej linke', prejdete z tohto uzla do 'normálneho jazdného pruhu' pomocou ukazovateľa a keď budete hľadať uzol na normálnej linke.
Preskočiť zoznam základných operácií
V zozname preskočení sú nasledujúce typy operácií.
Algoritmus operácie vkladania
Insertion (L, Key) local update [0...Max_Level + 1] a = L → header for i = L → level down to 0 do. while a → forward[i] → key forward[i] update[i] = a a = a → forward[0] lvl = random_Level() if lvl > L → level then for i = L → level + 1 to lvl do update[i] = L → header L → level = lvl a = makeNode(lvl, Key, value) for i = 0 to level do a → forward[i] = update[i] → forward[i] update[i] → forward[i] = a
Algoritmus operácie vymazania
Deletion (L, Key) local update [0... Max_Level + 1] a = L → header for i = L → level down to 0 do. while a → forward[i] → key forward[i] update[i] = a a = a → forward[0] if a → key = Key then for i = 0 to L → level do if update[i] → forward[i] ? a then break update[i] → forward[i] = a → forward[i] free(a) while L → level > 0 and L → header → forward[L → level] = NIL do L → level = L → level - 1
Algoritmus operácie vyhľadávania
Searching (L, SKey) a = L → header loop invariant: a → key level down to 0 do. while a → forward[i] → key forward[i] a = a → forward[0] if a → key = SKey then return a → value else return failure
Príklad 1: Vytvorte zoznam preskočení, chceme vložiť tieto nasledujúce kľúče do prázdneho zoznamu preskočení.
- 6 s úrovňou 1.
- 29 s úrovňou 1.
- 22 s úrovňou 4.
- 9 s úrovňou 3.
- 17 s úrovňou 1.
- 4 s úrovňou 2.
Roky:
Krok 1: Vložte 6 s úrovňou 1

Krok 2: Vložte 29 s úrovňou 1

Krok 3: Vložte 22 s úrovňou 4

Krok 4: Vložte 9 s úrovňou 3

Krok 5: Vložte 17 s úrovňou 1

Krok 6: Vložte 4 s úrovňou 2

Príklad 2: Zvážte tento príklad, kde chceme hľadať kľúč 17.

Roky:

Výhody zoznamu preskočenia
- Ak chcete vložiť nový uzol do zoznamu preskočení, potom sa uzol vloží veľmi rýchlo, pretože v zozname preskočenia nie sú žiadne rotácie.
- Preskakovací zoznam je jednoduchý na implementáciu v porovnaní s hašovacou tabuľkou a binárnym vyhľadávacím stromom.
- Je veľmi jednoduché nájsť uzol v zozname, pretože ukladá uzly v zoradenej forme.
- Algoritmus preskakovacieho zoznamu možno veľmi jednoducho upraviť v špecifickejšej štruktúre, ako sú indexovateľné zoznamy preskočení, stromy alebo prioritné fronty.
- Zoznam preskočení je robustný a spoľahlivý zoznam.
Nevýhody zoznamu preskočenia
- Vyžaduje viac pamäte ako vyvážený strom.
- Spätné vyhľadávanie nie je povolené.
- Preskakovací zoznam prehľadáva uzol oveľa pomalšie ako prepojený zoznam.
Aplikácie zoznamu Preskočiť
- Používa sa v distribuovaných aplikáciách a predstavuje ukazovatele a systém v distribuovaných aplikáciách.
- Používa sa na implementáciu dynamického elastického súbežného frontu s nízkym súperením o uzamknutie.
- Používa sa aj s triedou šablón QMap.
- Indexovanie zoznamu preskočení sa používa pri problémoch so spúšťaním mediánu.
- Preskakovací zoznam sa používa na uverejňovanie delta-kódovania pri vyhľadávaní v Lucene.
