Newtonov zákon chladenia je základný zákon, ktorý popisuje rýchlosť prenosu tepla telesom do jeho okolia prostredníctvom žiarenia. Tento zákon hovorí, že rýchlosť, ktorou teleso vyžaruje teplo, je priamo úmerná rozdielu teplôt telesa od jeho okolia, keďže rozdiel teplôt je nízky. čím vyšší je rozdiel medzi teplotou tela a jeho okolia, tým viac tepla sa stráca a čím nižšia je teplota, tým menej tepla sa stráca. Newtonov zákon chladenia je špeciálnym prípadom Stefan-Boltzmannovho zákona.

V tomto článku sa podrobne dozvieme o Newtonovom zákone chladenia, vzorci Newtonovho zákona o chladení, jeho odvodení, príkladoch a ďalších.

Definícia Newtonovho zákona chladenia

Newton bol prvý, kto študoval vzťah medzi teplom, ktoré telo stráca do svojho okolia. Uvádza, že čím väčší je rozdiel v teplote medzi objektom a jeho okolím, tým viac tepla telo vyžaruje.

Newtonov zákon chladenia uvádza, že

Rýchlosť tepelných strát z telesa je priamo úmerná rozdielu teplôt medzi telesom a jeho okolím, vzhľadom na to, že teplotný rozdiel nie je veľký.

Tento zákon sa používa na vysvetlenie, prečo horúca voda alebo mlieko ponechané na stole vychladnú rýchlejšie ako trochu teplého mlieka alebo vody ponechané na stole. Newtonov zákon ochladzovania nám pomáha zistiť teplotu kohokoľvek bez toho, aby sme ju skutočne merali, vzhľadom na počiatočnú teplotu tela a teplotu okolia.

Vzorec Newtonovho zákona chladenia

Vzorec Newtonovho zákona chladenia je vzorec na výpočet teploty materiálu, ktorý stráca teplo do svojho okolia žiarením.

Podľa Newtonovho zákona ochladzovania

Rýchlosť tepelných strát ( – dQ/dt) telesa je priamo úmerná rozdielu teplôt [AT = (T ₂ – T ₁ )] tela a okolia.

mockito kedykoľvek

Môžeme to reprezentovať ako,

– dQ/dt ∝ (T ₂ – T ₁ )

– dQ/dt = k(T ₂ – T ₁ )

kde,
k je konštanta úmernosti

Vyriešením vyššie uvedenej diferenciálnej rovnice dostaneme,

T(t) = T _s + (T _O – T _s ) To je ^-kt

kde,
t je čas
T(t) je teplota Telesa v čase t
T _s je okolitá teplota
T _O je počiatočná telesná teplota
k je konštanta úmernosti

Odvodenie Newtonovho zákona ochladzovania

Vzorec Newtonovho zákona chladenia možno odvodiť pomocou riešenia diferenciálnej rovnice. Nech má teleso s hmotnosťou m so špecifickou tepelnou kapacitou s teplotu T₂a T₁je teplota okolia.

Ak teplota klesne o malé množstvo dT ₂ na čas dt , potom množstvo strateného tepla je,

dQ = ms dT ₂

Rýchlosť tepelných strát je daná,

dQ/dt = ms (dT ₂ /dt)

Podľa Newtonovho zákona ochladzovania

– dQ/dt = k(T ₂ – T ₁ )

Porovnanie vyššie uvedenej rovnice

– ms (dT ₂ /dt) = k (T ₂ – T ₁ )

vkladanie triediť java

dT ₂ /(T ₂ –T ₁ ) = – (k / ms) dt

dT ₂ /(T ₂ – T ₁ ) = – Kdt

kde, K = k/ms

Integrácia vyššie uvedenej rovnice

log _{to je} (T ₂ – T ₁ ) = – Kt + c

T ₂ = T ₁ + C“ a ^–Kt

kde, C' = e ^c

Vzťah medzi poklesom teploty tela a časom je znázornený pomocou grafu ochladzovania. Sklon tohto grafu ukazuje rýchlosť poklesu teploty.

Krivka ochladzovania je graf, ktorý znázorňuje vzťah medzi telesnou teplotou a časom. Rýchlosť poklesu teploty je určená sklonom dotyčnice ku krivke v ľubovoľnom bode. Obrázok pridaný nižšie ukazuje pokles teploty a časový vzťah.

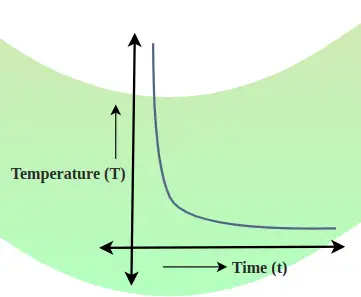
Všeobecne,

T(t) = T _A +(T _H -T _A )To je ^-kt

kde
T(t) je Teplota v čase t
T _A je okolitá teplota alebo teplota okolia
T _H je teplota horúceho predmetu
k je kladná konštanta a t je čas

Metódy aplikácie Newtonovho zákona ochladzovania

Pri konštantnej rýchlosti ochladzovania sa rýchlosť ochladzovania vzťahuje na priemernú teplotu tela počas intervalu, potom môžeme vypočítať približnú hodnotu pomocou Newtonovho zákona ochladzovania.

dθ/dt = k(q – q _s )

kde,
q je telesná teplota
q _s je teplota okolia

Ak je teda priemerná teplota telesa q, kde,

q = (q _i + q _f )/2

Overenie Newtonovho zákona chladenia

Newtonov zákon chladenia môžeme ľahko overiť experimentom opísaným nižšie:

V experimente vezmeme dvojstennú nádobu (V) s vodou medzi dve steny. Do dvojstennej nádoby naberieme medený kalorimeter (C) s horúcou vodou.

Používame dva teplomery T₂na meranie teploty vody v kalorimetri a T₁na meranie teploty teplej vody medzi dvojitými stenami. Po rovnakých časových intervaloch sa zaznamenajú obe teploty a graf medzi log_{to je}(T₂–T₁) a čas (t), ktorý sa zobrazí ako priamka so záporným sklonom.

Graf Newtonovho zákona chladenia

Nižšie je pridaný graf Newtonovho zákona chladenia, v tomto grafe je zobrazený logaritmus rozdielu medzi dvoma teplotami a časom.

Obmedzenia Newtonovho zákona chladenia

Rôzne obmedzenia Newtonovho zákona chladenia sú,

• Newtonov zákon chladenia platí, ak je teplotný rozdiel medzi telom a prostredím malý.
• Straty tepla organizmom sú iba vo forme Žiarenie .
• Teplota okolia musí počas ochladzovania tela zostať konštantná, ak nie, potom neplatí Newtonov zákon chladenia.

Aplikácia Newtonovho zákona chladenia

Rôzne aplikácie Newtonovho zákona chladenia sú,

• Odhadnúť, ako dlho bude teplý objekt trvať, kým sa ochladí na určitú teplotu.
• Určenie teploty nápoja v chladničke po uplynutí určitého času.
• Pomáha indikovať čas smrti pohľadom na možnú telesnú teplotu v čase smrti a aktuálnu telesnú teplotu.

Čítaj viac,

• Špecifická tepelná kapacita
• Základný pojem termodynamiky
• Termodynamické procesy

Vyriešené príklady Newtonov zákon chladenia

Príklad 1: Panvica naplnená horúcim jedlom sa ochladí z 94 °C na 86 °C za 2 minúty, keď je izbová teplota 20 °C. Ako dlho bude trvať, kým sa ochladí zo 71 °C na 69 °C?

Riešenie:

Priemer 94 °C a 86 °C je 90 °C,

• T₂= 90 °C
• T₁= 20 °C

Drop in tem. jedlo má 8 °C za 2 minúty.

Podľa Newtonovho zákona chladenia,

– dQ/dt = k(T ₂ –T ₁ )

8 °C /2 min = k(90 – 20)

4 = k(70) …………(1)

reťazec na celé číslo v jazyku Java

Priemer 69 °C a 71 °C je 70 °C

• T₂= 70 °C
• T₁= 20 °C

Podľa Newtonovho zákona ochladzovania

2 °C /dt = k(70 – 20) ……(2)

Z rovnice (1) a (2),

Zmena času = 0,7 min = = 42 sek

To znamená, že jedlo bude trvať 42 sekúnd, kým sa ochladí zo 71 °C na 69 °C.

Príklad 2: Teleso s teplotou 40ºC je udržiavané v prostredí s konštantnou teplotou 20ºC. Pozoruje sa, že jeho teplota klesne na 35ºC za 10 minút. Zistite, koľko času ešte potrvá, kým telo dosiahne teplotu 30ºC.

Riešenie:

Vzhľadom na to,

• q_i= (40 – 20) °C
• q_f= (35 – 20)ºC

Podľa Newtonovho zákona chladenia

q _f = q _i to je ^-kt

Teraz pre interval, v ktorom teplota klesne zo 40 ºC na 35 ºC.

(35 – 20) = (40 – 20) a^-(10k)

to je^{-10 tis}= 3/4

-10k = (ln 4/3)

k = 0,2876/10

k = 0,02876

Teraz znova používam Newonov vzorec,

(30 – 20) = (35 – 20)e^-kt

10 = 15e^-kt

to je^-kt= 23

-kt = ln(2/3)

t = 0,40546/k

java otváranie súboru

Pomocou hodnoty k,

t = 0,40546/0,02876

t = 14,098 min

Čas, ktorý telo potrebuje na dosiahnutie teploty 30ºC, je teda 14,098 min.

Príklad 3: Olej sa zahreje na 70 °C. Po 6 minútach sa ochladí na 50 ºC. Vypočítajte čas potrebný na ochladenie oleja z 50 ºC na 40 ºC vzhľadom na okolitú teplotu T _s = 25 °C

Riešenie:

Vzhľadom na to,

Teplota oleja po 6 minútach t.j. T(t) sa rovná 50 ºC

• Teplota okolia T_s= 25 °C
• Teplota oleja, T_O= 70 °C
• Čas na ochladenie na 50 °C = 6 minút

Podľa Newtonovho zákona ochladzovania

T(t) = T_s+ (T₀– T_s) To je^-kt

{T(t) – T_s}/(T_O– T_s) = a^-kt

-kt = ln[(T(t) – T_s)/(T_O– T_s)] ………(1)

Nahraďte hodnoty

-kt = ln[(50 – 25)/(70 – 25)]

-k = (ln 0,55556)/6

k = 0,09796

Priemerná teplota od 50 ºC do 40 ºC sa rovná 45 ºC

Opäť pomocou Newtonovho zákona chladenia

-(0,09796)t = ln[(45 – 25)/(70 – 25)]

-0,09796t = ln(0,44444)

0,09796t = 0,81093

t = 0,09796/0,58778 = 8,278 min

Čas potrebný na ochladenie oleja z 50 ºC na 40 ºC je teda 8,278 min

Príklad 4: Voda sa zahrieva na 80 °C počas 10 minút. Aká by bola jeho teplota v stupňoch Celzia, ak k = 0,056 za minútu a okolitá teplota je 25 ºC?

Riešenie:

Vzhľadom na to,

• Teplota okolia T_s= 25 °C
• Teplota vody T₀= 80 °C
• Čas, počas ktorého sa voda ohrieva (t) = 10 min
• Hodnota konštanty k = 0,056.

Podľa Newtonovho zákona ochladzovania

T(t) = T_s+ (T₀– T_s) To je^-kt

Nahradením hodnoty

T(t)= 25 + (80 – 25)e^-(0,056×10)

T(t) = 25 + 55 e^-(0,056×10)

string int

T(t) = 25 + 31,42

T(t) = 56,42

Po 10 minútach by mala byť teplota vody 56,42 °C.

Časté otázky o Newtonovom zákone chladenia

Otázka 1: Čo je Newtonov zákon chladenia?

odpoveď:

Newtonov zákon chladenia hovorí, že miera tepelných strát telesa je priamo úmerná rozdielu teplôt medzi telesom a jeho okolím.

Otázka 2: Aký je vzorec Newtonovho zákona o chladení?

odpoveď:

Vzorec Newtonovho zákona chladenia hovorí, že

T(t) = T _s + (T _O – T _s ) To je ^-kt

Otázka 3: Čo je k v Newtonovom zákone chladenia?

odpoveď:

The k vo vzorci Newtonovho zákona chladenia je konštanta, ktorá závisí od materiálu, t. j. zmena materiálu mení k v Newtonovom zákone chladenia.

Otázka 4: Prečo sa horúce mlieko ľahšie pije z misky ako z pohára?

odpoveď:

Miska má väčší povrch ako sklo, preto viac tepla stráca do svojho okolia vo forme sálania tepla cez misku, a preto je pre nás jednoduchšie piť horúce mlieko z misky.