V reálnom svete strojové učenie aplikáciách, je bežné, že má veľa relevantných funkcií, ale pozorovateľná môže byť len podmnožina z nich. Pri práci s premennými, ktoré sú niekedy pozorovateľné a niekedy nie, je skutočne možné využiť prípady, keď je táto premenná viditeľná alebo pozorovaná, aby sme sa naučili a robili predpovede pre prípady, keď nie je pozorovateľná. Tento prístup sa často označuje ako manipulácia s chýbajúcimi údajmi. Použitím dostupných prípadov, v ktorých je premenná pozorovateľná, sa algoritmy strojového učenia môžu naučiť vzory a vzťahy z pozorovaných údajov. Tieto naučené vzory sa potom môžu použiť na predpovedanie hodnôt premennej v prípadoch, keď chýba alebo nie je pozorovateľná.
Algoritmus očakávania-maximalizácie možno použiť na zvládnutie situácií, keď sú premenné čiastočne pozorovateľné. Keď sú určité premenné pozorovateľné, môžeme tieto prípady použiť na učenie a odhad ich hodnôt. Potom môžeme predpovedať hodnoty týchto premenných v prípadoch, keď to nie je možné pozorovať.
Algoritmus EM bol navrhnutý a pomenovaný v kľúčovom článku publikovanom v roku 1977 Arthurom Dempsterom, Nan Lairdom a Donaldom Rubinom. Ich práca formalizovala algoritmus a demonštrovala jeho užitočnosť pri štatistickom modelovaní a odhadoch.
EM algoritmus je použiteľný pre latentné premenné, čo sú premenné, ktoré nie sú priamo pozorovateľné, ale sú odvodené z hodnôt iných pozorovaných premenných. Využitím známej všeobecnej formy rozdelenia pravdepodobnosti, ktorou sa riadia tieto latentné premenné, môže EM algoritmus predpovedať ich hodnoty.
Algoritmus EM slúži ako základ pre mnoho nekontrolovaných klastrovacích algoritmov v oblasti strojového učenia. Poskytuje rámec na nájdenie lokálnych parametrov maximálnej pravdepodobnosti štatistického modelu a odvodenie latentných premenných v prípadoch, keď údaje chýbajú alebo sú neúplné.
Algoritmus očakávanej maximalizácie (EM).
Algoritmus Expectation-Maximization (EM) je iteratívna optimalizačná metóda, ktorá kombinuje rôzne nekontrolované strojové učenie algoritmy na nájdenie maximálnej pravdepodobnosti alebo maximálnych zadných odhadov parametrov v štatistických modeloch, ktoré zahŕňajú nepozorované latentné premenné. Algoritmus EM sa bežne používa pre modely latentných premenných a dokáže spracovať chýbajúce údaje. Pozostáva z kroku odhadu (E-krok) a kroku maximalizácie (M-krok), ktoré tvoria iteračný proces na zlepšenie prispôsobenia modelu.
- V kroku E algoritmus vypočítava latentné premenné, t. j. očakávanie logaritmickej pravdepodobnosti pomocou aktuálnych odhadov parametrov.
- V kroku M algoritmus určuje parametre, ktoré maximalizujú očakávanú logaritmickú pravdepodobnosť získanú v kroku E, a zodpovedajúce parametre modelu sa aktualizujú na základe odhadovaných latentných premenných.

Očakávania-maximalizácia v EM algoritme
Iteratívnym opakovaním týchto krokov sa EM algoritmus snaží maximalizovať pravdepodobnosť pozorovaných údajov. Bežne sa používa na učebné úlohy bez dozoru, ako je klastrovanie, kde sa odvodzujú latentné premenné a má uplatnenie v rôznych oblastiach vrátane strojového učenia, počítačového videnia a spracovania prirodzeného jazyka.
Kľúčové pojmy v algoritme maximalizácie očakávaní (EM).
Niektoré z najčastejšie používaných kľúčových pojmov v algoritme Expectation-Maximization (EM) sú nasledovné:
- Latentné premenné: Latentné premenné sú nepozorované premenné v štatistických modeloch, ktoré možno odvodiť len nepriamo prostredníctvom ich účinkov na pozorovateľné premenné. Nedajú sa priamo merať, ale možno ich zistiť na základe ich vplyvu na pozorovateľné premenné. Pravdepodobnosť: Je to pravdepodobnosť pozorovania daných údajov vzhľadom na parametre modelu. V EM algoritme je cieľom nájsť parametre, ktoré maximalizujú pravdepodobnosť. Log-pravdepodobnosť: Je to logaritmus pravdepodobnostnej funkcie, ktorý meria vhodnosť zhody medzi pozorovanými údajmi a modelom. Algoritmus EM sa snaží maximalizovať logaritmickú pravdepodobnosť. Odhad maximálnej pravdepodobnosti (MLE): MLE je metóda na odhadovanie parametrov štatistického modelu nájdením hodnôt parametrov, ktoré maximalizujú funkciu pravdepodobnosti, ktorá meria, ako dobre model vysvetľuje pozorované údaje. Posteriorná pravdepodobnosť: V kontexte Bayesovskej inferencie môže byť EM algoritmus rozšírený na odhad maximálnych a posteriori (MAP) odhadov, kde je zadná pravdepodobnosť parametrov vypočítaná na základe predchádzajúceho rozdelenia a pravdepodobnostnej funkcie. Krok očakávania (E): Krok E EM algoritmu vypočítava očakávanú hodnotu alebo neskoršiu pravdepodobnosť latentných premenných na základe pozorovaných údajov a aktuálnych odhadov parametrov. Zahŕňa výpočet pravdepodobnosti každej latentnej premennej pre každý údajový bod. Maximalizačný (M) krok: M-krok EM algoritmu aktualizuje odhady parametrov maximalizáciou očakávanej logaritmickej pravdepodobnosti získanej z E-kroku. Zahŕňa nájdenie hodnôt parametrov, ktoré optimalizujú funkciu pravdepodobnosti, zvyčajne pomocou numerických optimalizačných metód. Konvergencia: Konvergencia sa týka stavu, keď EM algoritmus dosiahol stabilné riešenie. Zvyčajne sa určuje kontrolou, či zmena logaritmickej pravdepodobnosti alebo odhadov parametrov neklesne pod vopred definovaný prah.
Ako funguje algoritmus Expectation-Maximization (EM):
Podstatou algoritmu Expectation-Maximization je použitie dostupných pozorovaných údajov súboru údajov na odhad chýbajúcich údajov a následné použitie týchto údajov na aktualizáciu hodnôt parametrov. Poďme pochopiť EM algoritmus podrobne.
java string nahradenie

Vývojový diagram EM algoritmu
- Inicializácia:
- Na začiatku sa berie do úvahy súbor počiatočných hodnôt parametrov. Súbor neúplných pozorovaných údajov je daný systému s predpokladom, že pozorované údaje pochádzajú z konkrétneho modelu.
- Vypočítajte zadnú pravdepodobnosť alebo zodpovednosť každej latentnej premennej na základe pozorovaných údajov a aktuálnych odhadov parametrov.
- Odhadnite chýbajúce alebo neúplné hodnoty údajov pomocou aktuálnych odhadov parametrov.
- Vypočítajte logaritmickú pravdepodobnosť pozorovaných údajov na základe aktuálnych odhadov parametrov a odhadovaných chýbajúcich údajov.
- Aktualizujte parametre modelu maximalizáciou očakávanej pravdepodobnosti úplného záznamu údajov získanej z E-kroku.
- To zvyčajne zahŕňa riešenie optimalizačných problémov s cieľom nájsť hodnoty parametrov, ktoré maximalizujú logaritmickú pravdepodobnosť.
- Konkrétna použitá optimalizačná technika závisí od povahy problému a použitého modelu.
- Skontrolujte konvergenciu porovnaním zmeny logaritmickej pravdepodobnosti alebo hodnôt parametrov medzi iteráciami.
- Ak je zmena pod vopred definovanou prahovou hodnotou, zastavte sa a považujte algoritmus za konvergovaný.
- V opačnom prípade sa vráťte k E-kroku a opakujte proces, kým sa nedosiahne konvergencia.
Implementácia algoritmu na maximalizáciu očakávaní krok za krokom
Importujte potrebné knižnice
Python3
import> numpy as np> import> matplotlib.pyplot as plt> from> scipy.stats>import> norm> |
čo je používateľské meno
>
>
Vytvorte množinu údajov s dvoma gaussovskými komponentmi
Python3
# Generate a dataset with two Gaussian components> mu1, sigma1>=> 2>,>1> mu2, sigma2>=> ->1>,>0.8> X1>=> np.random.normal(mu1, sigma1, size>=>200>)> X2>=> np.random.normal(mu2, sigma2, size>=>600>)> X>=> np.concatenate([X1, X2])> # Plot the density estimation using seaborn> sns.kdeplot(X)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.show()> |
>
>
Výkon :
porovnať s javou

Graf hustoty
Inicializujte parametre
Python3
# Initialize parameters> mu1_hat, sigma1_hat>=> np.mean(X1), np.std(X1)> mu2_hat, sigma2_hat>=> np.mean(X2), np.std(X2)> pi1_hat, pi2_hat>=> len>(X1)>/> len>(X),>len>(X2)>/> len>(X)> |
>
>
Vykonajte EM algoritmus
- Iteruje pre zadaný počet epoch (v tomto prípade 20).
- V každej epoche E-krok vypočíta zodpovednosť (hodnoty gama) vyhodnotením gaussovských hustôt pravdepodobnosti pre každú zložku a ich vážením zodpovedajúcimi proporciami.
- M-krok aktualizuje parametre výpočtom váženého priemeru a štandardnej odchýlky pre každý komponent
Python3
df.loc
# Perform EM algorithm for 20 epochs> num_epochs>=> 20> log_likelihoods>=> []> for> epoch>in> range>(num_epochs):> ># E-step: Compute responsibilities> >gamma1>=> pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >gamma2>=> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)> >total>=> gamma1>+> gamma2> >gamma1>/>=> total> >gamma2>/>=> total> > ># M-step: Update parameters> >mu1_hat>=> np.>sum>(gamma1>*> X)>/> np.>sum>(gamma1)> >mu2_hat>=> np.>sum>(gamma2>*> X)>/> np.>sum>(gamma2)> >sigma1_hat>=> np.sqrt(np.>sum>(gamma1>*> (X>-> mu1_hat)>*>*>2>)>/> np.>sum>(gamma1))> >sigma2_hat>=> np.sqrt(np.>sum>(gamma2>*> (X>-> mu2_hat)>*>*>2>)>/> np.>sum>(gamma2))> >pi1_hat>=> np.mean(gamma1)> >pi2_hat>=> np.mean(gamma2)> > ># Compute log-likelihood> >log_likelihood>=> np.>sum>(np.log(pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >+> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)))> >log_likelihoods.append(log_likelihood)> # Plot log-likelihood values over epochs> plt.plot(>range>(>1>, num_epochs>+>1>), log_likelihoods)> plt.xlabel(>'Epoch'>)> plt.ylabel(>'Log-Likelihood'>)> plt.title(>'Log-Likelihood vs. Epoch'>)> plt.show()> |
>
>
Výkon :

Pravdepodobnosť epochy vs log
Nakreslite konečnú odhadovanú hustotu
Python3
vypnite režim vývojára
# Plot the final estimated density> X_sorted>=> np.sort(X)> density_estimation>=> pi1_hat>*>norm.pdf(X_sorted,> >mu1_hat,> >sigma1_hat)>+> pi2_hat>*> norm.pdf(X_sorted,> >mu2_hat,> >sigma2_hat)> plt.plot(X_sorted, gaussian_kde(X_sorted)(X_sorted), color>=>'green'>, linewidth>=>2>)> plt.plot(X_sorted, density_estimation, color>=>'red'>, linewidth>=>2>)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.legend([>'Kernel Density Estimation'>,>'Mixture Density'>])> plt.show()> |
>
>
Výkon :
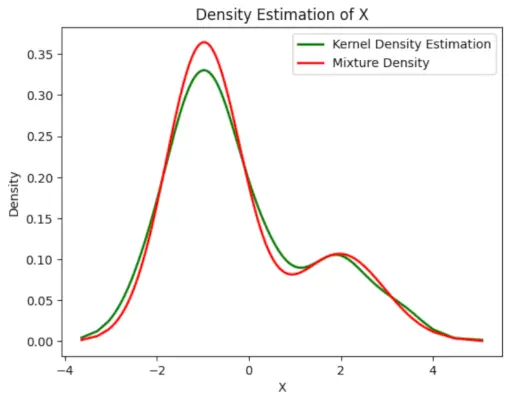
Odhadovaná hustota
Aplikácie EM algoritmus
- Môže sa použiť na doplnenie chýbajúcich údajov vo vzorke.
- Môže byť použitý ako základ nekontrolovaného učenia sa klastrov.
- Môže sa použiť na účely odhadu parametrov skrytého Markovovho modelu (HMM).
- Môže sa použiť na zisťovanie hodnôt latentných premenných.
Výhody EM algoritmu
- Vždy je zaručené, že pravdepodobnosť sa bude zvyšovať s každou iteráciou.
- E-krok a M-krok sú často veľmi jednoduché pre mnohé problémy z hľadiska implementácie.
- Riešenia M-krokov často existujú v uzavretej forme.
Nevýhody EM algoritmu
- Má pomalú konvergenciu.
- Dosahuje len konvergenciu k lokálnemu optimu.
- Vyžaduje obe pravdepodobnosti, doprednú aj spätnú (numerická optimalizácia vyžaduje iba doprednú pravdepodobnosť).
