Dané pole arr[] ktorý predstavuje a Kompletný binárny strom t.j. ak index i je rodič index 2*i + 1 je ľavé dieťa a index 2*i + 2 je správne dieťa. Úlohou je nájsť minimálne počet swapy potrebné na jeho premenu na a Binárny vyhľadávací strom.
Príklady:
Vstup: arr[] = [5 6 7 8 9 10 11]
výstup: 3
Vysvetlenie:
Binárny strom daného poľa:

Výmena 1: Vymeňte uzol 8 za uzol 5.
Výmena 2: Vymeňte uzol 9 za uzol 10.
Výmena 3: Vymeňte uzol 10 za uzol 7.Na získanie nižšie uvedeného binárneho vyhľadávacieho stromu sú teda potrebné minimálne 3 swapy:
if else príkazy java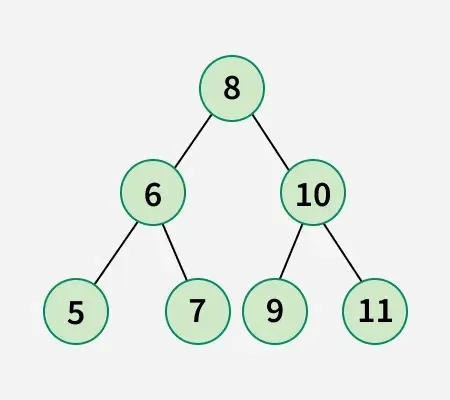
Vstup: arr[] = [1 2 3]
výstup: 1
Vysvetlenie:
Binárny strom daného poľa: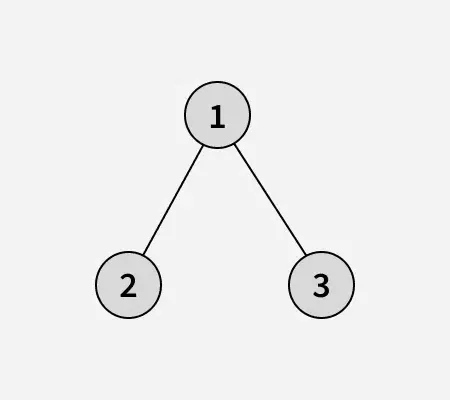
Po výmene uzla 1 s uzlom 2 získajte nižšie uvedený binárny vyhľadávací strom:
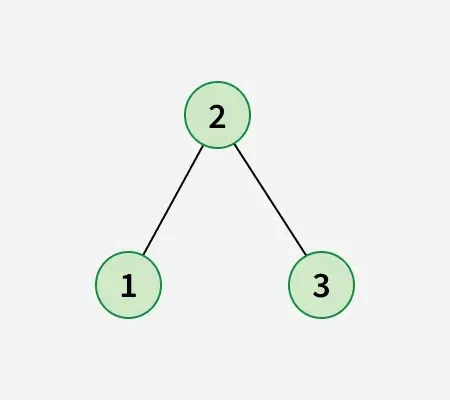
Prístup:
C++Cieľom je využiť túto skutočnosť neriadený prechod z Binárny vyhľadávací strom je v zvyšujúci sa poradie ich hodnoty.
Takže nájdite neriadený prechod binárneho stromu a uložte ho do poľa a snažiť sa triediť pole. The minimálny počet swapov potrebných na zoradenie poľa bude odpoveď.
// C++ program for Minimum swap required // to convert binary tree to binary search tree #include
// Java program for Minimum swap required // to convert binary tree to binary search tree import java.util.Arrays; class GfG { // Function to perform inorder traversal of the binary tree // and store it in an array static void inorder(int[] arr int[] inorderArr int index int[] counter) { int n = arr.length; // Base case: if index is out of bounds return if (index >= n) return; // Recursively visit left subtree inorder(arr inorderArr 2 * index + 1 counter); // Store current node value in the inorder array inorderArr[counter[0]] = arr[index]; counter[0]++; // Recursively visit right subtree inorder(arr inorderArr 2 * index + 2 counter); } // Function to calculate minimum swaps // to sort inorder traversal static int minSwaps(int[] arr) { int n = arr.length; int[] inorderArr = new int[n]; int[] counter = new int[1]; // Get the inorder traversal of the binary tree inorder(arr inorderArr 0 counter); // Create an array of pairs to store the value // and its original index int[][] t = new int[n][2]; int ans = 0; // Store the value and its original index for (int i = 0; i < n; i++) { t[i][0] = inorderArr[i]; t[i][1] = i; } // Sort the array based on values to get BST order Arrays.sort(t (a b) -> Integer.compare(a[0] b[0])); // Find minimum swaps by detecting cycles boolean[] visited = new boolean[n]; // Iterate through the array to find cycles for (int i = 0; i < n; i++) { // If the element is already visited or in // the correct place continue if (visited[i] || t[i][1] == i) continue; // Start a cycle and find the number of // nodes in the cycle int cycleSize = 0; int j = i; while (!visited[j]) { visited[j] = true; j = t[j][1]; cycleSize++; } // If there is a cycle we need (cycleSize - 1) // swaps to sort the cycle if (cycleSize > 1) { ans += (cycleSize - 1); } } // Return the total number of swaps return ans; } public static void main(String[] args) { int[] arr = {5 6 7 8 9 10 11}; System.out.println(minSwaps(arr)); } }
# Python program for Minimum swap required # to convert binary tree to binary search tree # Function to perform inorder traversal of the binary tree # and store it in an array def inorder(arr inorderArr index): # If index is out of bounds return n = len(arr) if index >= n: return # Recursively visit left subtree inorder(arr inorderArr 2 * index + 1) # Store current node value in inorderArr inorderArr.append(arr[index]) # Recursively visit right subtree inorder(arr inorderArr 2 * index + 2) # Function to calculate minimum swaps # to sort inorder traversal def minSwaps(arr): inorderArr = [] # Get the inorder traversal of the binary tree inorder(arr inorderArr 0) # Create a list of pairs to store value and original index t = [(inorderArr[i] i) for i in range(len(inorderArr))] ans = 0 # Sort the list of pairs based on values # to get BST order t.sort() # Initialize visited array visited = [False] * len(t) # Find minimum swaps by detecting cycles for i in range(len(t)): # If already visited or already in the # correct place skip if visited[i] or t[i][1] == i: continue # Start a cycle and find the number of # nodes in the cycle cycleSize = 0 j = i # Process all elements in the cycle while not visited[j]: visited[j] = True j = t[j][1] cycleSize += 1 # If there is a cycle of size `cycle_size` we # need `cycle_size - 1` swaps if cycleSize > 1: ans += (cycleSize - 1) # Return total number of swaps return ans if __name__ == '__main__': arr = [5 6 7 8 9 10 11] print(minSwaps(arr))
// C# program for Minimum swap required // to convert binary tree to binary search tree using System; using System.Linq; class GfG { // Function to perform inorder traversal of the binary tree // and store it in an array static void Inorder(int[] arr int[] inorderArr int index ref int counter) { int n = arr.Length; // Base case: if index is out of bounds return if (index >= n) return; // Recursively visit left subtree Inorder(arr inorderArr 2 * index + 1 ref counter); // Store current node value in inorderArr inorderArr[counter] = arr[index]; counter++; // Recursively visit right subtree Inorder(arr inorderArr 2 * index + 2 ref counter); } // Function to calculate minimum // swaps to sort inorder traversal static int MinSwaps(int[] arr) { int n = arr.Length; int[] inorderArr = new int[n]; int counter = 0; // Get the inorder traversal of the binary tree Inorder(arr inorderArr 0 ref counter); // Create an array of pairs to store value // and original index var t = new (int int)[n]; for (int i = 0; i < n; i++) { t[i] = (inorderArr[i] i); } // Sort the array based on values to get BST order Array.Sort(t (a b) => a.Item1.CompareTo(b.Item1)); // Initialize visited array bool[] visited = new bool[n]; int ans = 0; // Find minimum swaps by detecting cycles for (int i = 0; i < n; i++) { // If already visited or already in // the correct place skip if (visited[i] || t[i].Item2 == i) continue; // Start a cycle and find the number // of nodes in the cycle int cycleSize = 0; int j = i; // Process all elements in the cycle while (!visited[j]) { visited[j] = true; j = t[j].Item2; cycleSize++; } // If there is a cycle of size `cycle_size` we // need `cycle_size - 1` swaps if (cycleSize > 1) { ans += (cycleSize - 1); } } // Return total number of swaps return ans; } static void Main(string[] args) { int[] arr = { 5 6 7 8 9 10 11 }; Console.WriteLine(MinSwaps(arr)); } }
// Javascript program for Minimum swap required // to convert binary tree to binary search tree // Inorder traversal to get values in sorted order function inorder(arr inorderArr index) { // If index is out of bounds return if (index >= arr.length) return; // Recursively visit left subtree inorder(arr inorderArr 2 * index + 1); // Store current node value in array inorderArr.push(arr[index]); // Recursively visit right subtree inorder(arr inorderArr 2 * index + 2); } // Function to calculate minimum swaps to sort inorder // traversal function minSwaps(arr) { let inorderArr = []; // Get the inorder traversal of the binary tree inorder(arr inorderArr 0); // Create an array of pairs to store value and original // index let t = inorderArr.map((val i) => [val i]); let ans = 0; // Sort the pair array based on values to get BST order t.sort((a b) => a[0] - b[0]); // Find minimum swaps by detecting cycles let visited = Array(arr.length) .fill(false); for (let i = 0; i < t.length; i++) { // If the element is already in the correct // position continue if (visited[i] || t[i][1] === i) continue; // Otherwise perform swaps until the element is in // the right place let cycleSize = 0; let j = i; while (!visited[j]) { visited[j] = true; j = t[j][1]; cycleSize++; } // If there is a cycle we need (cycleSize - 1) // swaps to sort the cycle if (cycleSize > 1) { ans += (cycleSize - 1); } } // Return total number of swaps return ans; } let arr = [ 5 6 7 8 9 10 11 ]; console.log(minSwaps(arr));
Výstup
3
Časová zložitosť: O(n*logn) kde n je počet prvkov v poli.
Pomocný priestor: O(n), pretože používa ďalší priestor pre pole
definovať počítač
Cvičenie: Môžeme to rozšíriť na normálny binárny strom, tj binárny strom reprezentovaný pomocou ľavého a pravého ukazovateľa a nemusí byť nevyhnutne úplný?
Vytvoriť kvíz



