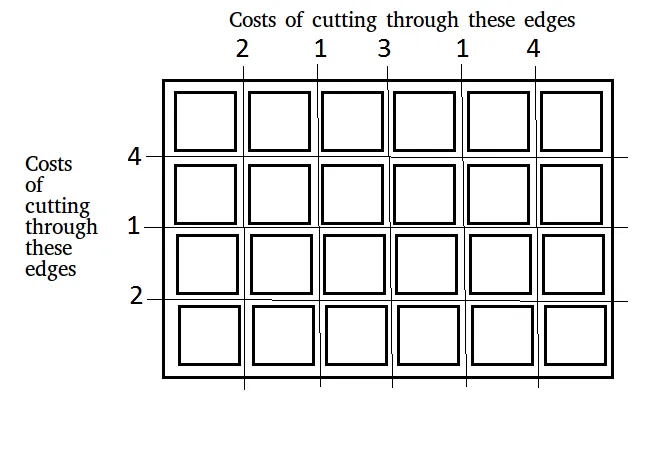
Vzhľadom na tabuľu rozmerov n × m ktoré je potrebné rozrezať na n × m štvorcov. Náklady na vykonanie rezu pozdĺž vodorovného alebo zvislého okraja sa poskytujú v dvoch poliach:

• x[] : Zníženie nákladov pozdĺž zvislých hrán (po dĺžke).
• a[] : Zníženie nákladov pozdĺž vodorovných okrajov (na šírku).

Nájdite minimálne celkové náklady potrebné na optimálne rozrezanie dosky na štvorce.

Príklady: 

Vstup: x[] = [2 1 3 1 4] y[] = [4 1 2] n = 4 m = 6
výstup: 42
Vysvetlenie:

Spočiatku nie. horizontálnych segmentov = 1 a č. zvislých segmentov = 1.
Optimálny spôsob rezu na štvorec je:
Vyberte 4 (z x) -> vertikálny rez Cena = 4 × horizontálne segmenty = 4
 Teraz horizontálne segmenty = 1 vertikálne segmenty = 2.
Vyberte 4 (z y) -> horizontálny rez Cena = 4 × zvislé segmenty = 8
 Teraz horizontálne segmenty = 2 vertikálne segmenty = 2.
Vyberte 3 (z x) -> vertikálny rez Cena = 3 × horizontálne segmenty = 6
 Teraz horizontálne segmenty = 2 vertikálne segmenty = 3.
Vyberte 2 (z x) -> vertikálny rez Cena = 2 × horizontálne segmenty = 4
 Teraz horizontálne segmenty = 2 vertikálne segmenty = 4.
Vyberte 2 (z y) -> horizontálny rez Cena = 2 × zvislé segmenty = 8
 Teraz horizontálne segmenty = 3 vertikálne segmenty = 4.
Vyberte 1 (z x) -> vertikálny rez Cena = 1 × horizontálne segmenty = 3
Teraz horizontálne segmenty = 3 vertikálne segmenty = 5.
Vyberte 1 (z x) -> vertikálny rez Cena = 1 × horizontálne segmenty = 3
Teraz horizontálne segmenty = 3 vertikálne segmenty = 6.
Vyberte 1 (z y) -> horizontálny rez Cena = 1 × zvislé segmenty = 6
Teraz horizontálne segmenty = 4 vertikálne segmenty = 6.
Takže celkové náklady = 4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42.

Vstup: x[] = [1 1 1] y[] = [1 1 1] n = 4 m = 4
výstup: 15
Vysvetlenie:
Spočiatku nie. horizontálnych segmentov = 1 a č. zvislých segmentov = 1.
Optimálny spôsob rezu na štvorec je:
Vyberte 1 (z y) -> horizontálny rez Cena = 1 × zvislé segmenty = 1
Teraz horizontálne segmenty = 2 vertikálne segmenty = 1.
Vyberte 1 (z y) -> horizontálny rez Cena = 1 × zvislé segmenty = 1
Teraz horizontálne segmenty = 3 vertikálne segmenty = 1.
Vyberte 1 (z y) -> horizontálny rez Cena = 1 × zvislé segmenty = 1
Teraz horizontálne segmenty = 4 vertikálne segmenty = 1.
Vyberte 1 (z x) -> vertikálny rez Cena = 1 × horizontálne segmenty = 4
Teraz horizontálne segmenty = 4 vertikálne segmenty = 2.
Vyberte 1 (z x) -> vertikálny rez Cena = 1 × horizontálne segmenty = 4
Teraz horizontálne segmenty = 4 vertikálne segmenty = 3.
Vyberte 1 (z x) -> vertikálny rez Cena = 1 × horizontálne segmenty = 4
Teraz horizontálne segmenty = 4 vertikálne segmenty = 4
Takže celkové náklady = 1 + 1 + 1 + 4 + 4 + 4 = 15.

Obsah

• [Naivný prístup] Vyskúšajte všetky permutácie – O((n+m)!×(n+m)) Čas a O(n+m) Priestor
• [Očakávaný prístup] Použitie chamtivej techniky - O( n (log n) + m (log m)) Čas a O (1) Priestor

[Naivný prístup] Vyskúšajte všetky permutácie – O((n+m)!×(n+m)) Čas a O(n+m) Priestor

Cieľom je vygenerovať všetky možné permutácie daných rezov a potom vypočítať náklady na každú permutáciu. Nakoniec medzi nich vráťte minimálne náklady.

Poznámka: Tento prístup nie je realizovateľný pre väčšie vstupy, pretože počet permutácií rastie faktoriálne ako (m+n-2)!.
Pre každú permutáciu musíme vypočítať náklady v O(m+n) čase. Celková časová zložitosť sa tak stáva O((m+n−2)!×(m+n)).

[Očakávaný prístup] Použitie chamtivej techniky - O( n (log n) + m (log m)) Čas a O (1) Priestor

Cieľom je najskôr urobiť najdrahšie rezy pomocou a zištný prístup . Pozorovaním je, že výber najvyššieho zníženia nákladov v každom kroku znižuje budúce náklady ovplyvnením viacerých kusov naraz. Zoraďujeme vertikálne (x) a horizontálne (y) znížené náklady v zostupnom poradí a potom opakovane vyberieme väčšie, aby sme maximalizovali úspory nákladov. Zvyšné rezy sa spracovávajú oddelene, aby sa zabezpečilo optimálne rozdelenie všetkých častí.

Čo sa stane, keď urobíme rez?

• Horizontálny rez → Režete po šírke, aby sa zvýšil počet vodorovných pásikov (hCount++). Náklady sa však vynásobia vCount (počet vertikálnych pásikov), pretože horizontálny rez musí prechádzať cez všetky vertikálne segmenty.
• Vertikálny rez → režete po výške, takže počet zvislých pásikov sa zvyšuje (vCount++). Náklady sa však vynásobia hCount (počet vodorovných pásov), pretože vertikálny rez musí prejsť všetkými horizontálnymi segmentmi.

Kroky na vyriešenie problému:

• Zoraďte polia x a y v zostupnom poradí.
• Použite dva ukazovatele, jeden pre x a jeden pre y, začínajúc od najväčšej hodnoty a postupujte smerom k menším hodnotám.
• Udržujte hodnoty hCount a vCount, aby ste mohli sledovať, koľko segmentov ovplyvňuje každý strih, a podľa toho ich aktualizujte.
• Opakujte, kým x a y majú nespracované škrty, vždy si vyberte väčšie náklady, aby ste minimalizovali celkové náklady.
• Ak x má zostávajúce rezy, spracujte ich pomocou násobiteľa hCount; podobne spracujte zostávajúce y rezy pomocou vCount.
• Zhromaždite celkové náklady v každom kroku pomocou vzorca: znížte náklady * počet ovplyvnených kusov, čím sa zabezpečia minimálne náklady.

#include   #include #include   using namespace std; int minCost(int n int m   vector<int>& x vector<int>& y) {    // Sort the cutting costs in ascending order  sort(x.begin() x.end());  sort(y.begin() y.end());   int hCount = 1 vCount = 1;   int i = x.size() - 1 j = y.size() - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } int main() {    int n = 4 m = 6;  vector<int> x = {2 1 3 1 4};  vector<int> y = {4 1 2};  cout << minCost(n m x y) << endl;  return 0; } 

import java.util.Arrays; class GfG {    static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Arrays.sort(x);  Arrays.sort(y);   int hCount = 1 vCount = 1;   int i = x.length - 1 j = y.length - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }  public static void main(String[] args) {    int n = 4m = 6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  System.out.println(minCost(n m x y));  } } 

def minCost(nm x y): # Sort the cutting costs in ascending order x.sort() y.sort() hCount vCount = 1 1 i j = len(x) - 1 len(y) - 1 totalCost = 0 while i >= 0 and j >= 0: # Choose the larger cost cut to  # minimize future costs if x[i] >= y[j]: totalCost += x[i] * hCount vCount += 1 i -= 1 else: totalCost += y[j] * vCount hCount += 1 j -= 1 # Process remaining vertical cuts while i >= 0: totalCost += x[i] * hCount vCount += 1 i -= 1 # Process remaining horizontal cuts while j >= 0: totalCost += y[j] * vCount hCount += 1 j -= 1 return totalCost if __name__ == '__main__': nm = 4 6 x = [2 1 3 1 4] y = [4 1 2] print(minCost(nmx y)) 

using System; class GfG {  public static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Array.Sort(x);  Array.Sort(y);  int hCount = 1 vCount = 1;  int i = x.Length - 1 j = y.Length - 1;  int totalCost = 0;  // Process the cuts in greedy manner  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }    public static void Main() {    int n=4m=6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  Console.WriteLine(minCost(nm x y));  } } 

function minCost( nm x y) {    // Sort the cutting costs in ascending order  x.sort((a b) => a - b);  y.sort((a b) => a - b);  let hCount = 1 vCount = 1;  let i = x.length - 1 j = y.length - 1;  let totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }   else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } // Driver Code let n = 4m = 6; let x = [2 1 3 1 4]; let y = [4 1 2]; console.log(minCost(nm x y)); 

42