Finite Automata (FA) je najjednoduchší stroj na rozpoznávanie vzorov. Používa sa na charakterizáciu regulárneho jazyka, napríklad: /baa+!/.
Používa sa tiež na analýzu a rozpoznávanie výrazov v prirodzenom jazyku. Konečný automat alebo konečný automat je abstraktný stroj, ktorý má päť prvkov alebo n-tic. Má súbor stavov a pravidiel na prechod z jedného stavu do druhého, ale závisí od použitého vstupného symbolu. Na základe stavov a sady pravidiel môže byť vstupný reťazec buď prijatý alebo odmietnutý. V podstate ide o abstraktný model digitálneho počítača, ktorý číta vstupný reťazec a mení jeho vnútorný stav v závislosti od aktuálneho vstupného symbolu. Každý automat definuje jazyk, t. j. množinu reťazcov, ktoré akceptuje. Nasledujúci obrázok zobrazuje niektoré základné funkcie všeobecnej automatizácie.
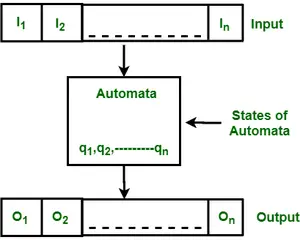
Obrázok: Funkcie Finite Automata
Vyššie uvedený obrázok ukazuje nasledujúce vlastnosti automatov:
- Vstup
- Výkon
- Stavy automatov
- Štátny vzťah
- Výstupný vzťah
Konečný automat pozostáva z nasledujúcich prvkov:
Q : Finite set of states. ? : set of Input Symbols. q : Initial state. F : set of Final States. ? : Transition Function.>
Formálna špecifikácia stroja je
premenná java
{ Q, ?, q, F, ? }> FA sa delí na dva typy:
1) Deterministické konečné automaty (DFA):
DFA consists of 5 tuples {Q, ?, q, F, ?}. Q : set of all states. ? : set of input symbols. ( Symbols which machine takes as input ) q : Initial state. ( Starting state of a machine ) F : set of final state. ? : Transition Function, defined as ? : Q X ? -->Otázka> V DFA pre konkrétny vstupný znak stroj prejde iba do jedného stavu. Pre každý stav je definovaná prechodová funkcia pre každý vstupný symbol. V DFA tiež nie je povolený nulový (alebo ?) presun, t. j. DFA nemôže zmeniť stav bez akéhokoľvek vstupného znaku.
Vytvorte napríklad DFA, ktorý akceptuje jazyk všetkých reťazcov končiacich na „a“.
Dané: ? = {a,b}, q = {q0}, F={q1}, Q = {q0, q1}
Najprv zvážte jazykovú sadu všetkých možných prijateľných reťazcov, aby ste vytvorili presný diagram prechodu stavu.
L = {a, aa, aaa, aaaa, aaaaa, ba, bba, bbba, otec, otec, otec, otec}
Vyššie je jednoduchá podmnožina možných prijateľných reťazcov, existuje mnoho ďalších reťazcov, ktoré končia na „a“ a obsahujú symboly {a,b}.
reťazcový formát java
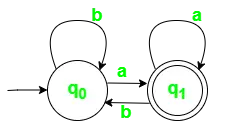
Obr 1. Stavový diagram prechodu pre DFA s ? = {a, b}
Neakceptované reťazce sú,
ab, bb, aab, abbb atď.
Tabuľka prechodu stavu pre vyššie uvedený automat,
| ?ŠtátSymbol? | a | b |
|---|---|---|
| q0 | q1 | q0 |
| q1 | q1 | q0 |
Jedna dôležitá vec, ktorú treba poznamenať, pre vzor môže byť veľa možných DFA . Všeobecne sa uprednostňuje DFA s minimálnym počtom stavov.
2) Nedeterministické konečné automaty (NFA): NFA je podobná DFA s výnimkou nasledujúcich dodatočných funkcií:
- Je povolený nulový (alebo ?) pohyb, tj môže sa pohybovať dopredu bez čítania symbolov.
- Schopnosť prenášať do ľubovoľného počtu stavov pre konkrétny vstup.
Tieto vyššie uvedené funkcie však NFA nepridávajú žiadnu silu. Ak porovnáme obe z hľadiska sily, obe sú rovnocenné.
Kvôli vyššie uvedeným dodatočným funkciám má NFA inú prechodovú funkciu, zvyšok je rovnaký ako DFA.
?: Transition Function ?: Q X (? U ? ) -->2 ^ Q.>
Ako môžete vidieť, funkcia prechodu je pre akýkoľvek vstup vrátane null (alebo?), NFA môže prejsť do ľubovoľného počtu stavov. Napríklad nižšie je NFA pre vyššie uvedený problém.
uzol zoznamu java
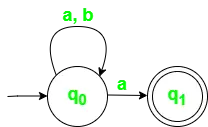
Obr 2. Stavový diagram prechodu pre NFA s ? = {a, b}
Tabuľka prechodu stavu pre vyššie uvedený automat,
| ?ŠtátSymbol? | a | b |
|---|---|---|
| q0 | {q0,q1} | q0 |
| q1 | ? | ? |
Jedna dôležitá vec, ktorú treba poznamenať, v NFA, ak nejaká cesta pre vstupný reťazec vedie do konečného stavu, potom vstupný reťazec je prijatý . Napríklad vo vyššie uvedenom NFA existuje viacero ciest pre vstupný reťazec 00. Keďže jedna z ciest vedie do konečného stavu, vyššie uvedený NFA akceptuje 00.
Niektoré dôležité body:
- Odôvodnenie:
In case of DFA ? : Q X ? -->Otázka V prípade NFA? : Q X? --> 2Q>
Teraz, keď budete pozorovať, zistíte Q X? –> Q je súčasťou Q X ? –> 2Q.
Na strane RHS je Q podmnožinou 2Qčo znamená, že Q je obsiahnuté v 2Qalebo Q je súčasťou 2Qopak však neplatí. Matematicky to teda môžeme uzavrieť každá DFA je NFA, ale nie naopak . Existuje však spôsob, ako previesť NFA na DFA, takže existuje ekvivalentná DFA pre každú NFA .
- NFA aj DFA majú rovnakú silu a každý NFA môže byť preložený do DFA.
- V DFA aj NFA môže existovať viacero konečných stavov.
- NFA je skôr teoretický koncept.
- DFA sa používa v Lexikálnej analýze v kompilátore.
- Ak je počet štátov v NFA N, potom jeho DFA môže mať maximálne 2Npočet štátov.
Pozrite si Kvíz o regulárnych výrazoch a konečných automatoch.
