Binárny vyhľadávací strom je dátová štruktúra používaná v informatike na organizovanie a ukladanie dát triedeným spôsobom. Binárny vyhľadávací strom sleduje všetky vlastnosti binárneho stromu a jeho vľavo dieťa obsahuje hodnoty menšie ako nadradený uzol a správny dieťa obsahuje hodnoty väčšie ako nadradený uzol. Táto hierarchická štruktúra umožňuje efektívnosť Hľadá sa , Vkladanie , a Vymazanie operácie s údajmi uloženými v strome.
Binárny vyhľadávací strom
Obsah
java a swing
- Čo je binárny vyhľadávací strom?
- Vlastnosti binárneho vyhľadávacieho stromu
- Spracovanie duplicitných hodnôt v strome binárneho vyhľadávania
- Operácie vykonávané na BST
- 1. Vyhľadávanie uzla v BST
- 2. Vložte uzol do BST
- 3. Vymažte uzol BST
- 4. Traversal (Inorder traversal BST)
- Aplikácie BST
- Výhody
- Nevýhody
- Často kladené otázky (často kladené otázky) o strome binárneho vyhľadávania:
Čo je binárny vyhľadávací strom?
Binárny vyhľadávací strom (BST) je špeciálny typ binárny strom v ktorom má ľavý potomok uzla hodnotu menšiu ako je hodnota uzla a pravý potomok má hodnotu väčšiu ako hodnota uzla. Táto vlastnosť sa nazýva vlastnosť BST a umožňuje efektívne vyhľadávať, vkladať a mazať prvky v strome.
Vlastnosti binárneho vyhľadávacieho stromu:
- Ľavý podstrom uzla obsahuje iba uzly s kľúčmi menšími ako kľúč uzla.
- Pravý podstrom uzla obsahuje iba uzly s kľúčmi väčšími ako kľúč uzla.
- To znamená, že všetko naľavo od koreňa je menšie ako hodnota koreňa a všetko napravo od koreňa je väčšie ako hodnota koreňa. Vďaka tomuto výkonu je binárne vyhľadávanie veľmi jednoduché.
- Ľavý a pravý podstrom musí byť tiež binárny vyhľadávací strom.
- Nesmú existovať žiadne duplicitné uzly (BST môže mať duplicitné hodnoty s rôznymi prístupmi k manipulácii)
Spracovanie duplicitných hodnôt v strome binárneho vyhľadávania:
- Počas celého procesu musíme postupovať konzistentne, t. j. buď uložiť duplicitnú hodnotu naľavo, alebo uložiť duplicitnú hodnotu napravo od koreňa, ale buďte konzistentní s vaším prístupom.
Základné operácie na strome binárneho vyhľadávania:
1. Vyhľadávanie uzla v BST:
Vyhľadávanie v BST znamená nájsť konkrétny uzol v dátovej štruktúre. V binárnom vyhľadávacom strome je vyhľadávanie uzla jednoduché, pretože má špecifické poradie. Kroky vyhľadávania uzla v strome binárneho vyhľadávania sú uvedené nasledovne –
- Najprv porovnajte prvok, ktorý sa má vyhľadávať, s koreňovým prvkom stromu.
- Ak sa root zhoduje s cieľovým prvkom, vráťte umiestnenie uzla.
- Ak sa nezhoduje, skontrolujte, či je položka menšia ako koreňový prvok, ak je menšia ako koreňový prvok, prejdite do ľavého podstromu.
- Ak je väčší ako koreňový prvok, prejdite do pravého podstromu.
- Opakujte vyššie uvedený postup rekurzívne, kým nenájdete zhodu.
- Ak sa prvok nenájde alebo sa v strome nenachádza, vráťte hodnotu NULL.
Teraz pochopme vyhľadávanie v binárnom strome pomocou príkladu:
Nižšie je uvedený BST a musíme hľadať prvok 6.
pripojenia v jave
kód:
Nižšie je implementácia vyhľadávania v BST:
C++ // C++ function to search a given key in a given BST #include using namespace std; struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = new struct node; temp->kľúč = položka; temp->left = temp->right = NULL; návratová teplota; } // Pomocná funkcia na vloženie // nového uzla s daným kľúčom v BST struct node* insert(struct node* node, int key) { // Ak je strom prázdny, vráti nový uzol if (node == NULL ) return newNode(key); // V opačnom prípade sa v strome zopakujte, ak (kľúč< node->key) node->left = insert(uzol->left, key); else if (kľúč> uzol->kľúč) uzol->vpravo = vložiť(uzol->vpravo, kľúč); // Vráti (nezmenený) ukazovateľ uzla return node; } // Pomôcka funkcia na vyhľadávanie kľúča v uzle štruktúry BST* search(struct node* root, kľúč int) root->key == kľúč) return root; // Kľúč je väčší ako koreňový kľúč if (root->key< key) return search(root->vpravo, kľúč); // Kľúč je menší ako kľúč roota return search(root->left, key);> C // C function to search a given key in a given BST #include #include struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc(sizeof(struct node)); temp->kľúč = položka; temp->left = temp->right = NULL; návratová teplota; } // Pomocná funkcia na vloženie // nového uzla s daným kľúčom v BST struct node* insert(struct node* node, int key) { // Ak je strom prázdny, vráti nový uzol if (node == NULL ) return newNode(key); // V opačnom prípade sa v strome zopakujte, ak (kľúč< node->key) node->left = insert(uzol->left, key); else if (kľúč> uzol->kľúč) uzol->vpravo = vložiť(uzol->vpravo, kľúč); // Vráti (nezmenený) ukazovateľ uzla return node; } // Funkcia pomôcky na vyhľadávanie kľúča v uzle štruktúry BST* vyhľadávanie (struct node* root, kľúč int)> Java // Java program to search a given key in a given BST class Node { int key; Node left, right; public Node(int item) { key = item; left = right = null; } } class BinarySearchTree { Node root; // Constructor BinarySearchTree() { root = null; } // A utility function to insert // a new node with given key in BST Node insert(Node node, int key) { // If the tree is empty, return a new node if (node == null) { node = new Node(key); return node; } // Otherwise, recur down the tree if (key < node.key) node.left = insert(node.left, key); else if (key>node.key) node.right = insert(uzol.right, key); // Vráti (nezmenený) ukazovateľ uzla return node; } // Funkcia pomôcky na vyhľadávanie kľúča pri vyhľadávaní uzla BST (koreň uzla, kľúč int) // Základné prípady: root je null alebo kľúč je prítomný v koreni if (root == null> Python # Python3 function to search a given key in a given BST class Node: # Constructor to create a new node def __init__(self, key): self.key = key self.left = None self.right = None # A utility function to insert # a new node with the given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Vráti (nezmenený) ukazovateľ uzla návratový uzol # Funkcia pomôcky na vyhľadávanie kľúča v BST def search(root, key): # Základné prípady: root je null alebo kľúč je prítomný v koreni, ak root je None alebo root.key == kľúč: return root # Kľúč je väčší ako root, ak root.key< key: return search(root.right, key) # Key is smaller than root's key return search(root.left, key)>
JavaScript // Javascript function to search a given key in a given BST class Node { constructor(key) { this.key = key; this.left = null; this.right = null; } } // A utility function to insert // a new node with given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node === null) { return new Node(key); } // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>uzol.kľúč) { uzol.vpravo = vložiť(uzol.vpravo, kľúč); } // Vráti (nezmenený) ukazovateľ uzla return node; } // Pomôcka funkcia na vyhľadávanie kľúča vo funkcii BST search(root, key) { // Základné prípady: root má hodnotu null alebo kľúč je prítomný v koreňovom adresári if (root === null || root.key === kľúč ) { return root; } // Kľúč je väčší ako koreňový kľúč if (root.key< key) { return search(root.right, key); } // Key is smaller than root's key return search(root.left, key); }>
2. Vložte uzol do BST :
Na krídlo sa vždy vloží nový kľúč. Začnite hľadať kľúč od koreňa po listový uzol. Po nájdení listového uzla sa nový uzol pridá ako potomok listového uzla.
kód:
Nižšie je uvedená implementácia vloženia jedného uzla do stromu binárneho vyhľadávania:
C++ // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->kľúč = položka; temp->left = temp->right = NULL; návratová teplota; } // Funkcia na vloženie nového uzla s // daným kľúčom v BST struct node* insert(struct node* node, int key) { // Ak je strom prázdny, vráti nový uzol if (node == NULL) return newNode(key); // V opačnom prípade sa v strome zopakujte, ak (kľúč< node->key) { uzol->left = insert(uzol->left, key); } else if (kľúč> uzol->kľúč) { uzol->vpravo = vložiť(uzol->vpravo, kľúč); } // Vráti ukazovateľ uzla return node; }> C // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->kľúč = položka; temp->left = temp->right = NULL; návratová teplota; } // Funkcia na vloženie nového uzla s // daným kľúčom v BST struct node* insert(struct node* node, int key) { // Ak je strom prázdny, vráti nový uzol if (node == NULL) return newNode(key); // V opačnom prípade sa v strome zopakujte, ak (kľúč< node->key) { uzol->left = insert(uzol->left, key); } else if (kľúč> uzol->kľúč) { uzol->vpravo = vložiť(uzol->vpravo, kľúč); } // Vráti ukazovateľ uzla return node; }> Java class GFG { // Given Node Structure static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>uzol.kľúč) { uzol.vpravo = vložiť(uzol.vpravo, kľúč); } // Vráti uzol návratový uzol; } }> Python3 # Given Node Structure class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Vráti ukazovateľ uzla návratový uzol>
Javascript // Given Node Structure class Node { constructor(key){ this.key = key; this.left = null; this.right = null; } } // Function to insert a new node with // given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node == null) return new Node(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>uzol.kľúč) { uzol.vpravo = vložiť(uzol.vpravo, kľúč); } // Vráti ukazovateľ uzla return node; }> Časová zložitosť: O(N), kde N je počet uzlov BST
Pomocný priestor: O(1)
3. Odstrániť uzol BST :
Používa sa na vymazanie uzla so špecifickým kľúčom z BST a vrátenie nového BST.
Rôzne scenáre na odstránenie uzla:
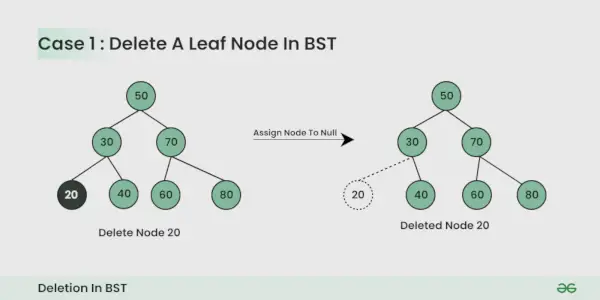
Uzol, ktorý sa má odstrániť, je listový uzol :
Je to jednoduché, môžete to jednoducho zrušiť.
mysql update join
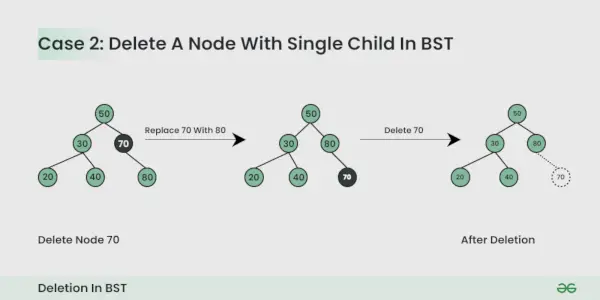
Uzol, ktorý sa má odstrániť, má jedného potomka :
Môžete jednoducho nahradiť uzol podriadeným uzlom.
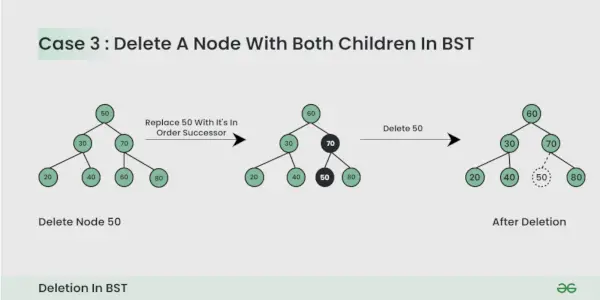
Uzol, ktorý sa má odstrániť, má dvoch potomkov :
Tu musíme delete the node je takým spôsobom, že výsledný strom sleduje vlastnosti BST. Trik je v nájdení poradového nástupcu uzla. Skopírujte obsah následníka poradia do uzla a vymažte následníka poradia.
Pri odstraňovaní uzla BST dbajte na nasledujúce veci:
- Je potrebné zistiť, čo bude náhradou uzla, ktorý sa má odstrániť.
- Chcete minimálne narušenie existujúcej stromovej štruktúry
- Môže prevziať náhradný uzol z ľavého alebo pravého podstromu odstránených uzlov.
- Ak berieme if z ľavého podstromu, musíme vziať najväčšiu hodnotu v ľavom podstrome.
- Ak berieme if z pravého podstromu, musíme vziať najmenšiu hodnotu v pravom podstrome.
kód:
Nižšie je uvedená implementácia odstránenia v BST:
C++ // C++ program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->kľúč = položka; temp->left = temp->right = NULL; návratová teplota; } // Funkcia na vloženie nového uzla s // daným kľúčom v BST struct node* insert(struct node* node, int key) { // Ak je strom prázdny, vráti nový uzol if (node == NULL) return newNode(key); // V opačnom prípade sa v strome zopakujte, ak (kľúč< node->key) { uzol->left = insert(uzol->left, key); } else if (kľúč> uzol->kľúč) { uzol->vpravo = vložiť(uzol->vpravo, kľúč); } // Vráti ukazovateľ uzla return node; } // Funkcia, ktorá vracia uzol s minimálnou // hodnotou kľúča nájdenou v tomto strome struct node* minValueNode(struct node* node) { struct node* current = node; // V slučke nadol nájdete list úplne vľavo while (aktuálny && aktuálny->ľavý != NULL) aktuálny = aktuálny->ľavý; spätný prúd; } // Funkcia, ktorá vymaže kľúč a // vráti novú koreňovú štruktúru node* deleteNode(struct node* root, int kľúč) { // base Case if (root == NULL) return root; // Ak je kľúč, ktorý sa má vymazať // menší ako koreňový kľúč, // potom leží v ľavom podstrome if (kľúč< root->kľúč) { root->left = deleteNode(root->left, key); } // Ak je kľúč, ktorý sa má odstrániť, // väčší ako kľúč koreňa, // potom leží v pravom podstrome else if (kľúč> root->kľúč) { root->right = deleteNode(root-> vpravo, kľúč); } // Ak je kľúč rovnaký ako kľúč root, // potom toto je uzol //, ktorý sa má odstrániť else { // Uzol s iba jedným potomkom // alebo bez potomka if (root->left == NULL) { struct node* temp = root->right; free(root); návratová teplota; } else if (root->right == NULL) { struct node* temp = root->left; free(root); návratová teplota; } // Uzol s dvoma potomkami: // Získanie nástupcu poradia (najmenší // v pravom podstrome) struct node* temp = minValueNode(root->right); // Skopírujte // obsah nasledovníka poradia do tohto uzla root->key = temp->key; // Vymazanie následníka poradia root->right = deleteNode(root->right, temp->key); } return root; }> C // C program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->kľúč = položka; temp->left = temp->right = NULL; návratová teplota; } // Funkcia na vloženie nového uzla s // daným kľúčom v BST struct node* insert(struct node* node, int key) { // Ak je strom prázdny, vráti nový uzol if (node == NULL) return newNode(key); // V opačnom prípade sa v strome zopakujte, ak (kľúč< node->key) { uzol->left = insert(uzol->left, key); } else if (kľúč> uzol->kľúč) { uzol->vpravo = vložiť(uzol->vpravo, kľúč); } // Vráti ukazovateľ uzla return node; } // Funkcia, ktorá vracia uzol s minimálnou // hodnotou kľúča nájdenou v tomto strome struct node* minValueNode(struct node* node) { struct node* current = node; // V slučke nadol nájdete list úplne vľavo while (aktuálny && aktuálny->ľavý != NULL) aktuálny = aktuálny->ľavý; spätný prúd; } // Funkcia, ktorá vymaže kľúč a // vráti novú koreňovú štruktúru node* deleteNode(struct node* root, int kľúč) { // base Case if (root == NULL) return root; // Ak je kľúč, ktorý sa má vymazať // menší ako koreňový kľúč, // potom leží v ľavom podstrome if (kľúč< root->kľúč) { root->left = deleteNode(root->left, key); } // Ak je kľúč, ktorý sa má odstrániť, // väčší ako kľúč koreňa, // potom leží v pravom podstrome else if (kľúč> root->kľúč) { root->right = deleteNode(root-> vpravo, kľúč); } // Ak je kľúč rovnaký ako kľúč root, // potom toto je uzol //, ktorý sa má odstrániť else { // Uzol s iba jedným potomkom // alebo bez potomka if (root->left == NULL) { struct node* temp = root->right; free(root); návratová teplota; } else if (root->right == NULL) { struct node* temp = root->left; free(root); návratová teplota; } // Uzol s dvoma potomkami: // Získanie nástupcu poradia (najmenší // v pravom podstrome) struct node* temp = minValueNode(root->right); // Skopírujte // obsah nasledovníka poradia do tohto uzla root->key = temp->key; // Vymazanie následníka poradia root->right = deleteNode(root->right, temp->key); } return root; }> Java // Java program for Delete a Node of BST class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>uzol.kľúč) { uzol.vpravo = vložiť(uzol.vpravo, kľúč); } // Vráti uzol návratový uzol; } // Funkcia, ktorá vracia uzol s minimálnou // hodnotou kľúča nájdenou v tomto strome statický uzol minValueNode(node node) { node current = node; // V slučke nadol nájdete list úplne vľavo while (current != null && current.left != null) current = current.left; spätný prúd; } // Funkcia, ktorá vymaže kľúč a // vráti nový koreňový statický uzol deleteNode(koreň uzla, kľúč int) { // base Case if (root == null) return root; // Ak je kľúč na vymazanie // menší ako koreňový kľúč, // potom leží v ľavom podstrome if (kľúč< root.key) { root.left = deleteNode(root.left, key); } // If the key to be deleted is // greater than the root's key, // then it lies in right subtree else if (key>root.key) { root.right = deleteNode(root.right, key); } // Ak je kľúč rovnaký ako kľúč root, // potom toto je uzol //, ktorý sa má odstrániť else { // Uzol s iba jedným potomkom // alebo bez potomka if (root.left == null) { teplota uzla = root.right; návratová teplota; } else if (root.right == null) { node temp = root.left; návratová teplota; } // Uzol s dvoma potomkami: // Získanie následníka poradia (najmenší // v pravom podstrome) node temp = minValueNode(root.right); // Skopírujte // obsah nasledovníka poradia do tohto uzla root.key = temp.key; // Vymazanie následníka poradia root.right = deleteNode(root.right, temp.key); } return root; }> Python # Python program to delete a node of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(root, key): # If the tree is empty, return a new node if root is None: return Node(key) # Otherwise, recur down the tree if key < root.key: root.left = insert(root.left, key) elif key>root.key: root.right = insert(root.right, key) # Vráti ukazovateľ uzla return root # Funkcia na vykonanie prechodu BST def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Funkcia, ktorá vracia uzol s minimálnou # hodnotou kľúča nájdenou v tomto strome def minValueNode(node): current = node # Slučka nadol a nájdenie listu úplne vľavo, kým je aktuálny a current.left is not None: current = current.left return current # Funkcia, ktorá vymaže kľúč a # vráti nový koreň def deleteNode(root, key): # base Case if root is None: return root # If the key to be delete je # menší ako koreňový kľúč, # potom leží v ľavom podstrome if< root.key: root.left = deleteNode(root.left, key) # If the key to be deleted is # greater than the root's key, # then it lies in right subtree elif key>root.key: root.right = deleteNode(root.right, key) # Ak je kľúč rovnaký ako kľúč root, # potom toto je uzol #, ktorý sa má odstrániť inak: # Uzol iba s jedným potomkom # alebo bez potomka ak root.left je None: temp = root.right root = None return temp elif root.right is None: temp = root.left root = Žiadny return temp # Uzol s dvoma potomkami: # Získaj nástupcu poradia (najmenší # v pravý podstrom) temp = minValueNode(root.right) # Skopírujte obsah následníka poradia # do tohto uzla root.key = temp.key # Vymažte následníka poradia root.right = deleteNode(root.right, temp.key) return root>
4. Traversal (Inorder traversal of BST) :
V prípade binárnych vyhľadávacích stromov (BST), Inorder traversal dáva uzly v neklesajúcom poradí. Najprv navštívime ľavé dieťa, potom koreň a potom pravé dieťa.
Nižšie je uvedená implementácia toho, ako vykonať postupné prechádzanie binárneho vyhľadávacieho stromu:
C++ // C++ program to implement // inorder traversal of BST #include using namespace std; // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->kľúč = položka; temp->left = temp->right = NULL; návratová teplota; } // Funkcia na vloženie nového uzla s // daným kľúčom v BST struct node* insert(struct node* node, int key) { // Ak je strom prázdny, vráti nový uzol if (node == NULL) return newNode(key); // V opačnom prípade sa v strome zopakujte, ak (kľúč< node->key) { uzol->left = insert(uzol->left, key); } else if (kľúč> uzol->kľúč) { uzol->vpravo = vložiť(uzol->vpravo, kľúč); } // Vráti ukazovateľ uzla return node; } // Funkcia na vykonanie prechodu BST podľa poradia void inorder(struct node* root) { if (root != NULL) { inorder(root->left); cout<< ' ' << root->kľúč; inorder(root->right); } } // Kód ovládača int main() { /* Vytvorme nasledujúci BST 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // Vytvorenie koreňa BST = insert(root, 50); vložiť(koreň, 30); vložiť(koreň, 20); vložiť(koreň, 40); vložiť(koreň, 70); vložiť(koreň, 60); vložiť(koreň, 80); // Volanie funkcie inorder(root); návrat 0; } // Tento kód prispel shivanisinghss2110> C // C program to implement // inorder traversal of BST #include #include // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->kľúč = položka; temp->left = temp->right = NULL; návratová teplota; } // Funkcia na vloženie nového uzla s // daným kľúčom v BST struct node* insert(struct node* node, int key) { // Ak je strom prázdny, vráti nový uzol if (node == NULL) return newNode(key); // V opačnom prípade sa v strome zopakujte, ak (kľúč< node->key) { uzol->left = insert(uzol->left, key); } else if (kľúč> uzol->kľúč) { uzol->vpravo = vložiť(uzol->vpravo, kľúč); } // Vráti ukazovateľ uzla return node; } // Funkcia na vykonanie prechodu BST podľa poradia void inorder(struct node* root) { if (root != NULL) { inorder(root->left); printf('%d ', root->key); inorder(root->right); } } // Kód ovládača int main() { /* Vytvorme nasledujúci BST 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // Vytvorenie koreňa BST = insert(root, 50); vložiť(koreň, 30); vložiť(koreň, 20); vložiť(koreň, 40); vložiť(koreň, 70); vložiť(koreň, 60); vložiť(koreň, 80); // Volanie funkcie inorder(root); návrat 0; }> Java import java.io.*; // Java program for Inorder Traversal class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>uzol.kľúč) { uzol.vpravo = vložiť(uzol.vpravo, kľúč); } // Vráti uzol návratový uzol; } // Funkcia na vykonanie prechodu BST staticky void inorder(koreň uzla) { if (koreň != null) { inorder(koreň.left); System.out.print(' ' + root.key); inorder(root.right); } } // Kód ovládača public static void main(String[] args) { /* Vytvorme nasledujúci BST 50 / 30 70 / / 20 40 60 80 */ node root = null; // vloženie hodnoty 50 root = insert(root, 50); // vloženie hodnoty 30 insert(root, 30); // vloženie hodnoty 20 insert(root, 20); // vloženie hodnoty 40 insert(root, 40); // vloženie hodnoty 70 insert(root, 70); // vloženie hodnoty 60 insert(root, 60); // vloženie hodnoty 80 insert(root, 80); // vypíše BST inorder(root); } } // Tento kód prispel abhijitjadhav1998> Python3 # Python program to implement # inorder traversal of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to create a new BST node def newNode(item): temp = Node(item) temp.key = item temp.left = temp.right = None return temp # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return newNode(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Vráti ukazovateľ uzla return node # Funkcia na vykonanie prechodu BST def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Driver Code if __name__ == '__main__': # Vytvorme nasledujúci BST # 50 # / # 30 70 # / / # 20 40 60 80 root = Žiadny # Vytvorenie koreňa BST = insert(koreň, 50) insert(koreň, 30) insert(koreň, 20) insert(koreň, 40) insert(koreň, 70) insert(koreň, 60) insert(koreň , 80) # Volanie funkcie inorder(root) #Tento kód prispel japmeet01>
Výkon
20 30 40 50 60 70 80>
Časová zložitosť: O(N), kde N je počet uzlov BST
Pomocný priestor: O(1)
pridanie reťazca java
Aplikácie BST:
- Algoritmy grafov: BST možno použiť na implementáciu grafových algoritmov, ako napríklad v algoritmoch s minimálnym spanning tree.
- Prioritné fronty: BST možno použiť na implementáciu prioritných frontov, kde prvok s najvyššou prioritou je v koreni stromu a prvky s nižšou prioritou sú uložené v podstrome.
- Samovyvažovací binárny vyhľadávací strom: BST môžu byť použité ako samovyvažujúce dátové štruktúry, ako je AVL strom a červeno-čierny strom.
- Ukladanie a získavanie údajov: BST možno použiť na rýchle ukladanie a získavanie údajov, ako napríklad v databázach, kde sa vyhľadávanie konkrétneho záznamu môže vykonávať v logaritmickom čase.
Výhody:
- Rýchle vyhľadávanie: Hľadanie konkrétnej hodnoty v BST má priemernú časovú zložitosť O(log n), kde n je počet uzlov v strome. Je to oveľa rýchlejšie ako hľadanie prvku v poli alebo prepojenom zozname, ktoré majú v najhoršom prípade časovú zložitosť O(n).
- Priebeh v poradí: BST je možné prechádzať v poradí, ktoré navštívi ľavý podstrom, koreň a pravý podstrom. Toto možno použiť na triedenie množiny údajov.
- Priestorovo efektívne: BST sú priestorovo efektívne, pretože na rozdiel od polí a prepojených zoznamov neukladajú žiadne nadbytočné informácie.
Nevýhody:
- Šikmé stromy: Ak sa strom vychýli, časová zložitosť operácií vyhľadávania, vkladania a vymazávania bude O(n) namiesto O(log n), čo môže spôsobiť, že strom bude neefektívny.
- Požadovaný dodatočný čas: Samovyvažovacie stromy vyžadujú dodatočný čas na udržanie rovnováhy počas operácií vkladania a odstraňovania.
- Účinnosť: BST nie sú efektívne pre množiny údajov s mnohými duplikátmi, pretože plytvajú priestorom.
Časté otázky(Často kladené otázky)na strome binárneho vyhľadávania:
1. Čo je binárny vyhľadávací strom?
Binárny vyhľadávací strom (BST) je binárny strom, kde každý uzol v ľavom podstrome je menší ako koreň a každý uzol v pravom podstrome má hodnotu väčšiu ako koreň . Vlastnosti binárneho vyhľadávacieho stromu sú rekurzívne: ak za koreň považujeme akýkoľvek uzol, tieto vlastnosti zostanú pravdivé.
2. Čo je operácia binárneho vyhľadávacieho stromu?
V strome binárneho vyhľadávania existujú tri hlavné operácie: 1. Vkladanie, 2. Mazanie, 3. Vyhľadávanie. Vďaka svojim vlastnostiam je efektívne hľadať akýkoľvek prvok v binárnom vyhľadávacom strome.
3. Čo je binárny vyhľadávací strom a strom AVL?
Binárny vyhľadávací strom : Binárny vyhľadávací strom (BST) je binárny strom, kde každý uzol v ľavom podstrome je menší ako koreň a každý uzol v pravom podstrome má hodnotu väčšiu ako koreň.
AVL strom : Binárne vyhľadávacie stromy (BST), ktoré sa automaticky vyrovnávajú a otáčajú, sú známe ako stromy AVL.
4. Aké sú využitie binárneho vyhľadávacieho stromu?
Binárne vyhľadávacie stromy je možné použiť na implementáciu abstraktných dátových typov ako napr dynamické množiny, vyhľadávacie tabuľky a prioritné fronty, a používa sa v triediace algoritmy ako napríklad triedenie stromov.
5. Aký je rozdiel medzi binárnym vyhľadávacím stromom a binárnym stromom?
Binárny vyhľadávací strom je strom, ktorý sa riadi určitým poradím na usporiadanie prvkov, zatiaľ čo binárny strom sa neriadi žiadnym poradím.
Súvisiace články:
- Aplikácia BST
- Aplikácie, výhody a nevýhody binárneho vyhľadávacieho stromu
- Vloženie do binárneho vyhľadávacieho stromu (BST)
- Vyhľadávanie v binárnom vyhľadávacom strome (BST)
- Odstránenie v binárnom vyhľadávacom strome (BST)
