Trojuholníky sú trojstranné uzavreté mnohouholníky tvorené priesečníkom troch čiar. V každodennom živote sa s tým stretávame veľa. Je to jeden zo základných tvarov geometrie. Má tri strany, tri uhly a tri vrcholy. Pravouhlý trojuholník je taký, v ktorom je jeden z uhlov vždy rovný 90°. Pythagorova veta je odvodený pre pravouhlé trojuholníky, ktorý hovorí, že druhá mocnina prepony (najdlhšia strana) sa rovná súčtu štvorcov základne a odvesny.

Vzhľadom na dĺžku aspoň dvoch strán pravouhlého trojuholníka môžeme nájsť hodnotu ľubovoľného uhla pravouhlého trojuholníka. Na tento účel používame rôzne goniometrické funkcie, ako sú sínus, kosínus, tangens, kotangens, sec a cosec. Tieto nám pomáhajú spojiť uhly pravouhlého trojuholníka s jeho stranami.

Vlastnosti

• Medzi tromi vrcholmi je vrchol pravého uhla
• Strana opačná k pravouhlému vrcholu sa nazýva hypotenzia .
• Dĺžka strán sa riadi Pytagorovou vetou, ktorá hovorí

hypotenzia ² = základňa ² + nadmorská výška ²

• Prepona je najdlhšia strana pravouhlého trojuholníka.
• Uhly iné ako pravý uhol sú ostré, pretože hodnota je menšia ako 90^O

Goniometrické funkcie

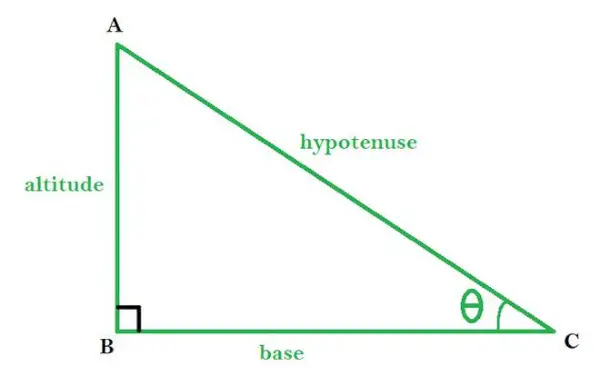
ABC je pravouhlý trojuholník s ∠B ako pravouhlým

bstrom a b strom

• cosθ: To dáva pomer základne s preponou pravouhlého trojuholníka.

cosθ = báza / prepona

• sinθ: To dáva pomer nadmorskej výšky podľa prepony pravouhlého trojuholníka.

sinθ = nadmorská výška / prepona

• tanθ: Je to pomer nadmorskej výšky k základni pravouhlého trojuholníka.

tanθ = nadmorská výška / základňa

• detská postieľkaθ: Je to prevrátená hodnota tanθ
• sekθ: Je to prevrátená hodnota cosθ
• cosecθ: Je to opak sinθ

Aby sme našli uhly pravouhlého trojuholníka, môžeme použiť trigonometrickú inverznú hodnotu pomeru daných strán trojuholníka.

Príklad:

Ak sinθ = x, potom môžeme písať

θ = hriech ^-1 X.

Toto vráti uhol, pre ktorý je sínusová hodnota uhla x.

Podobne existuje cos^-1θ, takže^-1ja, detská postieľka^-1θ, sek^-1θ a cosec^-1i

Ukážkové problémy

Otázka 1. Je daný pravouhlý trojuholník so základňou 10 cm a preponou 20 cm. Nájdite hodnotu základného uhla.

Riešenie:

Daná základňa = 10 cm

Prepona = 20 cm

Nech je hodnota základného uhla θ. Môžeme si písať

cosθ = základ / prepona = 10/20 = 1/2

θ = cos^-1(1/2) = 60^O

Hodnota základného uhla je teda 60 ^O .

Otázka 2. Nájdite hodnotu uhlov pravouhlého trojuholníka za predpokladu, že jeden z ostrých uhlov je dvojnásobkom druhého.

Riešenie:

Keďže vieme, že súčet všetkých troch uhlov v trojuholníku je 180^O.

Pretože jeden z uhlov je 90^Oa jeden z ostrých uhlov je dvojnásobkom druhého, môžeme ich považovať za θ a 2θ.

Takže môžeme písať

90^O+ 0 + 20 = 180^O

39 = 180^O– 90^O

30 = 90^O

0 = 90^O/3 = 30 ^O

20 = 2 x 30^O= 60 ^O

Takže uhly sú 30 ^O , 60 ^O , a 90 ^O .

Otázka 3. Nájdite hodnotu uhla elevácie rebríka dĺžky 5 m za predpokladu, že základňa rebríka je vo vzdialenosti 3 m od steny.

Riešenie:

Keďže rebrík funguje ako prepona pravouhlého trojuholníka a vzdialenosť základne je 3 m, môžeme písať

Prepona = 5m

Základňa = 3m

Nech je uhol elevácie θ. Takže môžeme písať

cosθ = základ / prepona = 3/5

θ = cos^-1(3/5)

0 = 53^O

Hodnota uhla elevácie je teda 53^O.

Otázka 4. Nájdite hodnotu prepony za predpokladu, že dĺžka nadmorskej výšky je 8 m a základný uhol sa rovná 30 ^O .

Riešenie:

Daný základný uhol sa rovná 30^Oa nadmorská výška sa rovná 8 m, môžeme použiť funkciu sínus na zistenie dĺžky prepony.

hriech30 ^O = nadmorská výška / prepona

prepona = nadmorská výška / sin30^O

Keďže hodnota hriechu30^Orovná sa 1/2, môžeme písať

prepona = nadmorská výška / (1/2) = 2 × nadmorská výška

Teda prepona = 2 × 8 = 16 m

Dĺžka prepony sa teda rovná 16 m.