logo

TechCodeview

Algoritmus Floyda Warshalla

The Floyd-Warshallov algoritmus , pomenovaná po svojich tvorcoch Robert Floyd a Stephen Warshall , je základným algoritmom v informatike a teórii grafov. Používa sa na nájdenie najkratších ciest medzi všetkými pármi uzlov vo váženom grafe. Tento algoritmus je vysoko efektívny a dokáže spracovať grafy s oboma pozitívne a n egatívne závažia hrán , čo z neho robí všestranný nástroj na riešenie širokého spektra problémov so sieťou a konektivitou.

Obsah



Floyd-Warshall-Algorithm-banner

Algoritmus Floyda Warshalla:

The Algoritmus Floyda Warshalla je na rozdiel od algoritmu najkratšej cesty všetkých párov Dijkstra a Bellman Ford čo sú jednozdrojové algoritmy najkratšej cesty. Tento algoritmus funguje pre obe riadený a neorientované vážené grafov. Ale nefunguje to pre grafy so zápornými cyklami (kde je súčet hrán v cykle záporný). Nasleduje to Dynamické programovanie prístup na kontrolu každej možnej cesty prechádzajúcej cez každý možný uzol, aby sa vypočítala najkratšia vzdialenosť medzi každým párom uzlov.

klávesnica o stránku nadol

Idea algoritmu Floyda Warshalla:

Predpokladajme, že máme graf G[][] s V vrcholy z 1 do N . Teraz musíme vyhodnotiť a shortestPathMatrix[][] kde je hortestPathMatrix[i][j] predstavuje najkratšiu cestu medzi vrcholmi i a j .



Jednoznačne najkratšia cesta medzi nimi i do j bude mať nejaké k počet medziľahlých uzlov. Myšlienkou algoritmu floyd warshall je ošetriť každý vrchol 1 do N ako medziľahlý uzol jeden po druhom.

Nasledujúci obrázok ukazuje vyššie uvedenú optimálnu vlastnosť subštruktúry v algoritme floyd warshall:

Algoritmus Floyd Warshall Algorithm:

  • Ako prvý krok inicializujte maticu riešenia rovnako ako maticu vstupného grafu.
  • Potom aktualizujte maticu riešenia tak, že všetky vrcholy budete považovať za stredný vrchol.
  • Cieľom je vybrať všetky vrcholy jeden po druhom a aktualizovať všetky najkratšie cesty, ktoré zahŕňajú vybratý vrchol ako medziľahlý vrchol v najkratšej ceste.
  • Keď vyberieme číslo vrcholu k ako stredný vrchol sme už uvažovali o vrcholoch {0, 1, 2, .. k-1} ako medziľahlé vrcholy.
  • Pre každý pár (i, j) zdrojových a cieľových vrcholov, existujú dva možné prípady.
    • k nie je medziľahlým vrcholom v najkratšej ceste z i do j . Zachovávame hodnotu dist[i][j] ako to je.
    • k je medziľahlý vrchol v najkratšej ceste od i do j . Aktualizujeme hodnotu dist[i][j] ako dist[i][k] + dist[k][j], ak dist[i][j]> dist[i][k] + dist[k][j]

Pseudokód algoritmu Floyda Warshalla:>

Pre k = 0 až n – 1
Pre i = 0 až n – 1
Pre j = 0 až n – 1
Vzdialenosť[i, j] = min(Vzdialenosť[i, j], Vzdialenosť[i, k] + Vzdialenosť[k, j])



reťazec java zreťaziť

kde i = zdrojový uzol, j = cieľový uzol, k = medziľahlý uzol

Ilustrácia Floyd Warshall Algorithm:

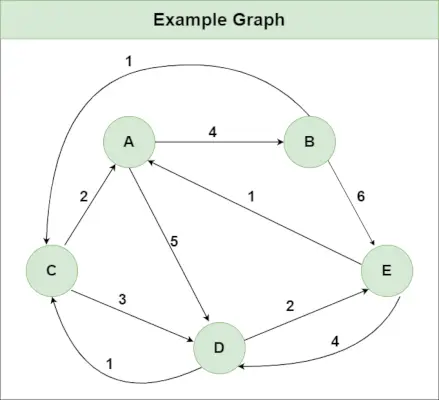
Predpokladajme, že máme graf, ako je znázornený na obrázku:

dryRun1drawio

Krok 1 : Inicializujte maticu Vzdialenosť[][] pomocou vstupného grafu tak, že Vzdialenosť[i][j]= hmotnosť hrany od i do j , tiež Vzdialenosť[i][j] = Nekonečno, ak neexistuje žiadna hrana z i do j.

step1drawio

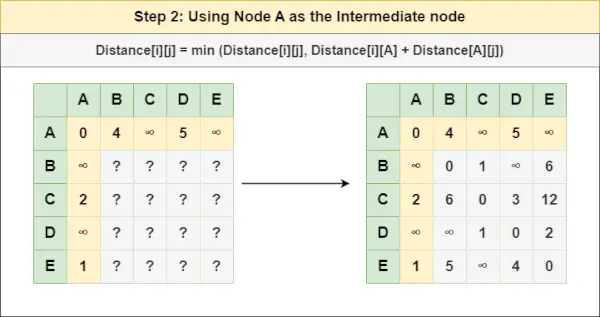
Krok 2 : Liečiť uzol A ako medziľahlý uzol a vypočítajte Vzdialenosť[][] pre každý pár uzlov {i,j} pomocou vzorca:

= Vzdialenosť[i][j] = minimum (Vzdialenosť[i][j], (Vzdialenosť od i do A ) + (Vzdialenosť od A až j))
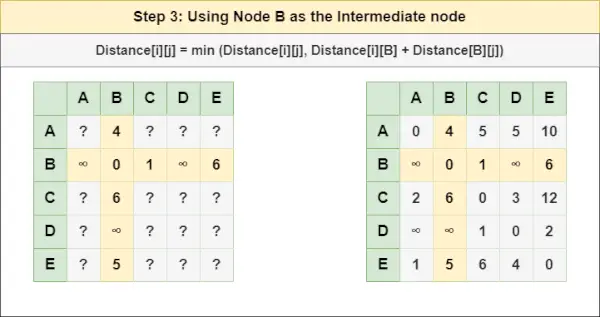
= Vzdialenosť[i][j] = minimum (Vzdialenosť[i][j], Vzdialenosť[i][ A ] + Vzdialenosť[ A ][j])

step2drawio

Krok 3 : Liečiť uzol B ako medziľahlý uzol a vypočítajte Vzdialenosť[][] pre každý pár uzlov {i,j} pomocou vzorca:

= Vzdialenosť[i][j] = minimum (Vzdialenosť[i][j], (Vzdialenosť od i do B ) + (Vzdialenosť od B až j))
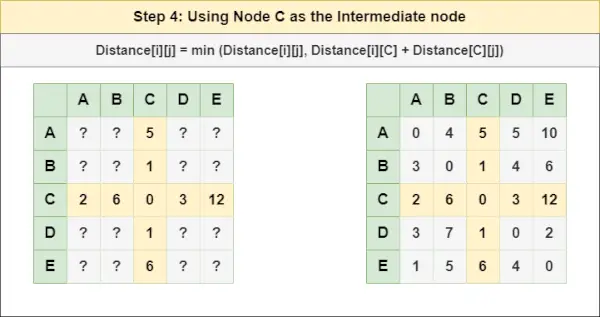
= Vzdialenosť[i][j] = minimum (Vzdialenosť[i][j], Vzdialenosť[i][ B ] + Vzdialenosť[ B ][j])

step3drawio

Krok 4 : Liečiť uzol C ako medziľahlý uzol a vypočítajte Vzdialenosť[][] pre každý pár uzlov {i,j} pomocou vzorca:

= Vzdialenosť[i][j] = minimum (Vzdialenosť[i][j], (Vzdialenosť od i do C ) + (Vzdialenosť od C až j))
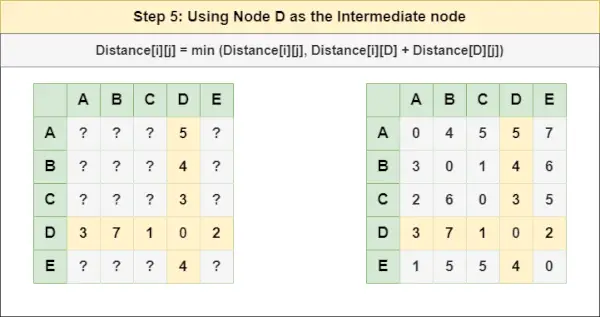
= Vzdialenosť[i][j] = minimum (Vzdialenosť[i][j], Vzdialenosť[i][ C ] + Vzdialenosť[ C ][j])

step4dravio

Krok 5 : Liečiť uzol D ako medziľahlý uzol a vypočítajte Vzdialenosť[][] pre každý pár uzlov {i,j} pomocou vzorca:

avl rotácia stromu

= Vzdialenosť[i][j] = minimum (Vzdialenosť[i][j], (Vzdialenosť od i do D ) + (Vzdialenosť od D až j))
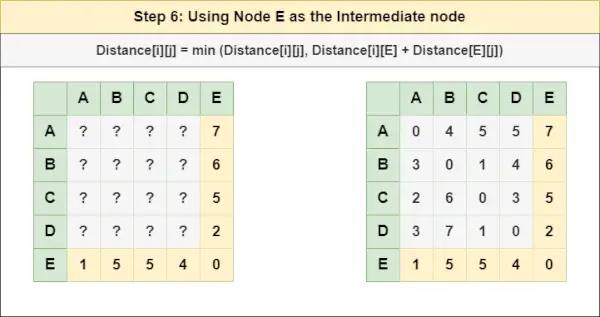
= Vzdialenosť[i][j] = minimum (Vzdialenosť[i][j], Vzdialenosť[i][ D ] + Vzdialenosť[ D ][j])

step5drawio

Krok 6 : Liečiť uzol A ako medziľahlý uzol a vypočítajte Vzdialenosť[][] pre každý pár uzlov {i,j} pomocou vzorca:

= Vzdialenosť[i][j] = minimum (Vzdialenosť[i][j], (Vzdialenosť od i do A ) + (Vzdialenosť od A až j))
= Vzdialenosť[i][j] = minimum (Vzdialenosť[i][j], Vzdialenosť[i][ A ] + Vzdialenosť[ A ][j])

step6drawio

Krok 7 : Keďže všetky uzly boli považované za prechodný uzol, teraz môžeme vrátiť aktualizovanú maticu Vzdialenosť[][] ako našu maticu odpovedí.

reťazcov na celé čísla
step7drawio
Odporúčaná prax Vyskúšajte to!

Nižšie je uvedená implementácia vyššie uvedeného prístupu:

C++ 
// C++ Program for Floyd Warshall Algorithm #include  using namespace std; // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value.This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) {  int i, j, k;  /* Add all vertices one by one to  the set of intermediate vertices.  --->Pred začiatkom iterácie máme najkratšie vzdialenosti medzi všetkými pármi vrcholov tak, že najkratšie vzdialenosti považujú iba vrcholy v množine {0, 1, 2, .. k-1} za stredné vrcholy.  ----> Po skončení iterácie sa vrchol č. k sa pridá k množine medziľahlých vrcholov a množina sa stane {0, 1, 2, .. k} */ pre (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path from  // i to j, then update the value of  // dist[i][j]  if (dist[i][j]>(dist[i][k] + dist[k][j]) && (dist[k][j] != INF && dist[i][k] != INF)) dist[i][j] = dist[i][k] + dist[k][j];  } } } // Tlač matice najkratšej vzdialenosti printSolution(dist); } /* Pomocná funkcia na tlač riešenia */ void printSolution(int dist[][V]) { cout<< 'The following matrix shows the shortest '  'distances'  ' between every pair of vertices 
';  for (int i = 0; i < V; i++) {  for (int j = 0; j < V; j++) {  if (dist[i][j] == INF)  cout << 'INF'  << ' ';  else  cout << dist[i][j] << ' ';  }  cout << endl;  } } // Driver's code int main() {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int graf[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } };  // Volanie funkcie floydWarshall(graph);  návrat 0; } // Tento kód prispel Mythri J L>
C 
// C Program for Floyd Warshall Algorithm #include  // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough  value. This value will be used  for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) {  int i, j, k;  /* Add all vertices one by one to  the set of intermediate vertices.  --->Pred začiatkom iterácie máme najkratšie vzdialenosti medzi všetkými pármi vrcholov tak, že najkratšie vzdialenosti považujú iba vrcholy v množine {0, 1, 2, .. k-1} za stredné vrcholy.  ----> Po skončení iterácie sa vrchol č. k sa pridá k množine medziľahlých vrcholov a množina sa stane {0, 1, 2, .. k} */ pre (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path from  // i to j, then update the value of  // dist[i][j]  if (dist[i][k] + dist[k][j] < dist[i][j])  dist[i][j] = dist[i][k] + dist[k][j];  }  }  }  // Print the shortest distance matrix  printSolution(dist); } /* A utility function to print solution */ void printSolution(int dist[][V]) {  printf(  'The following matrix shows the shortest distances'  ' between every pair of vertices 
');  for (int i = 0; i < V; i++) {  for (int j = 0; j < V; j++) {  if (dist[i][j] == INF)  printf('%7s', 'INF');  else  printf('%7d', dist[i][j]);  }  printf('
');  } } // driver's code int main() {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int graf[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } };  // Volanie funkcie floydWarshall(graph);  návrat 0; }>
Java 
// Java program for Floyd Warshall All Pairs Shortest // Path algorithm. import java.io.*; import java.lang.*; import java.util.*; class AllPairShortestPath {  final static int INF = 99999, V = 4;  void floydWarshall(int dist[][])  {  int i, j, k;  /* Add all vertices one by one  to the set of intermediate  vertices.  --->Pred začiatkom iterácie máme najkratšie vzdialenosti medzi všetkými pármi vrcholov tak, že najkratšie vzdialenosti považujú iba vrcholy v množine {0, 1, 2, .. k-1} za stredné vrcholy.  ----> Po skončení iterácie sa vrchol č. k sa pridá k množine medziľahlých vrcholov a množina sa stane {0, 1, 2, .. k} */ pre (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path  // from i to j, then update the value of  // dist[i][j]  if (dist[i][k] + dist[k][j]  < dist[i][j])  dist[i][j]  = dist[i][k] + dist[k][j];  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int dist[][])  {  System.out.println(  'The following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i][j] == INF)  System.out.print('INF ');  else  System.out.print(dist[i][j] + ' ');  }  System.out.println();  }  }  // Driver's code  public static void main(String[] args)  {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int graf[][] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } };  AllPairShortestPath a = new AllPairShortestPath();  // Volanie funkcie a.floydWarshall(graph);  } } // Prispel Aakash Hasija>
Python3 
# Python3 Program for Floyd Warshall Algorithm # Number of vertices in the graph V = 4 # Define infinity as the large # enough value. This value will be # used for vertices not connected to each other INF = 99999 # Solves all pair shortest path # via Floyd Warshall Algorithm def floydWarshall(graph):  ''' dist[][] will be the output   matrix that will finally  have the shortest distances   between every pair of vertices '''  ''' initializing the solution matrix   same as input graph matrix  OR we can say that the initial   values of shortest distances  are based on shortest paths considering no   intermediate vertices ''' dist = list(map(lambda i: list(map(lambda j: j, i)), graph))  ''' Add all vertices one by one   to the set of intermediate  vertices.  --->Pred začatím iterácie máme najkratšie vzdialenosti medzi všetkými pármi vrcholov tak, že za medziľahlé vrcholy sa považujú iba vrcholy v množine {0, 1, 2, .. k-1}.  ----> Po skončení iterácie sa vrchol č. k sa pridá do množiny medziľahlých vrcholov a množina sa stane {0, 1, 2, .. k} ''' pre k v rozsahu (V): # vybrať všetky vrcholy ako zdroj jeden po druhom pre i v range(V): # Vyberte všetky vrcholy ako cieľ pre # vyššie vybraný zdroj pre j v rozsahu (V): # Ak je vrchol k na najkratšej ceste z # i do j, potom aktualizujte hodnotu dist[i][ j] dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j] ) printSolution(dist) # Pomocná funkcia na tlač riešenia def printSolution (dist): print('Nasledujúca matica zobrazuje najkratšie vzdialenosti medzi každým párom vrcholov') pre i v rozsahu(V): pre j v rozsahu(V): if(dist[i][j] == INF): print('%7s' % ('INF'), end=' ') else: print('%7d	' % (dist[i][j]), end=' ') if j == V-1: print() # Kód vodiča if __name__ == '__main__': ''' 10 (0)------ ->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 ''' graf = [[0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0 , 1], [INF, INF, INF, 0] ] # Volanie funkcie floydWarshall(graph) # Tento kód prispel Mythri J L>
C# 
// C# program for Floyd Warshall All // Pairs Shortest Path algorithm. using System; public class AllPairShortestPath {  readonly static int INF = 99999, V = 4;  void floydWarshall(int[, ] graph)  {  int[, ] dist = new int[V, V];  int i, j, k;  // Initialize the solution matrix  // same as input graph matrix  // Or we can say the initial  // values of shortest distances  // are based on shortest paths  // considering no intermediate  // vertex  for (i = 0; i < V; i++) {  for (j = 0; j < V; j++) {  dist[i, j] = graph[i, j];  }  }  /* Add all vertices one by one to  the set of intermediate vertices.  --->Pred začiatkom iterácie máme najkratšie vzdialenosti medzi všetkými pármi vrcholov tak, že najkratšie vzdialenosti považujú iba vrcholy v množine {0, 1, 2, .. k-1} za stredné vrcholy.  ---> Po skončení iterácie sa vrchol č. k sa pridá k množine medziľahlých vrcholov a množina sa stane {0, 1, 2, .. k} */ pre (k = 0; k< V; k++) {  // Pick all vertices as source  // one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination  // for the above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest  // path from i to j, then update  // the value of dist[i][j]  if (dist[i, k] + dist[k, j]  < dist[i, j]) {  dist[i, j]  = dist[i, k] + dist[k, j];  }  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int[, ] dist)  {  Console.WriteLine(  'Following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i, j] == INF) {  Console.Write('INF ');  }  else {  Console.Write(dist[i, j] + ' ');  }  }  Console.WriteLine();  }  }  // Driver's Code  public static void Main(string[] args)  {  /* Let us create the following  weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int[, ] graf = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0 , 1 }, { INF, INF, INF, 0 } };  AllPairShortestPath a = new AllPairShortestPath();  // Volanie funkcie a.floydWarshall(graph);  } } // Autorom tohto článku je // Abdul Mateen Mohammed>
Javascript 
// A JavaScript program for Floyd Warshall All  // Pairs Shortest Path algorithm.  var INF = 99999;  class AllPairShortestPath {  constructor() {  this.V = 4;  }  floydWarshall(graph) {  var dist = Array.from(Array(this.V), () =>new Array(this.V).fill(0));  var i, j, k;  // Inicializujte maticu riešenia // rovnako ako vstupnú maticu grafu // Alebo môžeme povedať, že počiatočné // hodnoty najkratších vzdialeností // sú založené na najkratších cestách // bez ohľadu na medziľahlý // vrchol pre (i = 0; i< this.V; i++) {  for (j = 0; j < this.V; j++) {  dist[i][j] = graph[i][j];  }  }  /* Add all vertices one by one to  the set of intermediate vertices.  --->Pred začiatkom iterácie máme najkratšie vzdialenosti medzi všetkými pármi vrcholov tak, že najkratšie vzdialenosti považujú iba vrcholy v množine {0, 1, 2, .. k-1} za stredné vrcholy.  ---> Po skončení iterácie sa vrchol č. k sa pridá k množine medziľahlých vrcholov a množina sa stane {0, 1, 2, .. k} */ pre (k = 0; k< this.V; k++) {  // Pick all vertices as source  // one by one  for (i = 0; i < this.V; i++) {  // Pick all vertices as destination  // for the above picked source  for (j = 0; j < this.V; j++) {  // If vertex k is on the shortest  // path from i to j, then update  // the value of dist[i][j]  if (dist[i][k] + dist[k][j] < dist[i][j]) {  dist[i][j] = dist[i][k] + dist[k][j];  }  }  }  }  // Print the shortest distance matrix  this.printSolution(dist);  }  printSolution(dist) {  document.write(  'Following matrix shows the shortest ' +  'distances between every pair of vertices '  );  for (var i = 0; i < this.V; ++i) {  for (var j = 0; j < this.V; ++j) {  if (dist[i][j] == INF) {  document.write(' INF ');  } else {  document.write('  ' + dist[i][j] + ' ');  }  }  document.write(' ');  }  }  }  // Driver Code  /* Let us create the following  weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ var graf = [ [0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0, 1] , [INF, INF, INF, 0], ];  var a = new AllPairShortestPath();  // Tlač riešenia a.floydWarshall(graph);    // Tento kód prispel rdtaank.>
PHP 
 // PHP Program for Floyd Warshall Algorithm  // Solves the all-pairs shortest path problem // using Floyd Warshall algorithm  function floydWarshall ($graph, $V, $INF) { /* dist[][] will be the output matrix   that will finally have the shortest   distances between every pair of vertices */ $dist = array(array(0,0,0,0), array(0,0,0,0), array(0,0,0,0), array(0,0,0,0)); /* Initialize the solution matrix same   as input graph matrix. Or we can say the   initial values of shortest distances are   based on shortest paths considering no   intermediate vertex. */ for ($i = 0; $i < $V; $i++) for ($j = 0; $j < $V; $j++) $dist[$i][$j] = $graph[$i][$j]; /* Add all vertices one by one to the set   of intermediate vertices.   --->Pred začiatkom iterácie máme najkratšie vzdialenosti medzi všetkými pármi vrcholov tak, že najkratšie vzdialenosti považujú iba vrcholy v množine {0, 1, 2, .. k-1} za stredné vrcholy.   ----> Po skončení iterácie sa vrchol č. k sa pridá k množine medziľahlých vrcholov a množina sa zmení na {0, 1, 2, .. k} */ pre ($k = 0; $k< $V; $k++) { // Pick all vertices as source one by one  for ($i = 0; $i < $V; $i++) { // Pick all vertices as destination  // for the above picked source  for ($j = 0; $j < $V; $j++) { // If vertex k is on the shortest path from  // i to j, then update the value of dist[i][j]  if ($dist[$i][$k] + $dist[$k][$j] < $dist[$i][$j]) $dist[$i][$j] = $dist[$i][$k] + $dist[$k][$j]; } } } // Print the shortest distance matrix  printSolution($dist, $V, $INF); } /* A utility function to print solution */ function printSolution($dist, $V, $INF) { echo 'The following matrix shows the ' . 'shortest distances between ' . 'every pair of vertices 
'; for ($i = 0; $i < $V; $i++) { for ($j = 0; $j < $V; $j++) { if ($dist[$i][$j] == $INF) echo 'INF ' ; else echo $dist[$i][$j], ' '; } echo '
'; } } // Drivers' Code // Number of vertices in the graph  $V = 4 ; /* Define Infinite as a large enough  value. This value will be used for vertices not connected to each other */ $INF = 99999 ; /* Let us create the following weighted graph   10  (0)------->(3) | /| 5 | |   | | 1 |/ |  (1)------->(2) 3 */ $graf = pole(pole(0, 5, $INF, 10), pole($INF, 0, 3, $INF), pole($ INF, $INF, 0, 1), pole ($INF, $INF, $INF, 0)); // Volanie funkcie floydWarshall($graph, $V, $INF); // Tento kód prispel Ryuga ?>>
Výkon 
The following matrix shows the shortest distances between every pair of vertices 0 5 8 9 INF 0 3 4 INF INF 0 1 INF INF INF 0>

Analýza zložitosti algoritmu Floyd Warshall:

  • Časová zložitosť: O(V3), kde V je počet vrcholov v grafe a spustíme tri vnorené slučky, každú s veľkosťou V
  • Pomocný priestor: O(V2), na vytvorenie 2-D matice na uloženie najkratšej vzdialenosti pre každý pár uzlov.

Poznámka : Vyššie uvedený program tlačí len najkratšie vzdialenosti. Riešenie môžeme upraviť na tlač najkratších ciest aj uložením informácií o predchodcovi do samostatnej 2D matice.

Prečo je Floyd-Warshall Algorithm lepší pre husté grafy a nie pre riedke grafy?

Hustý graf : Graf, v ktorom je počet hrán výrazne vyšší ako počet vrcholov.
Riedky graf : Graf, v ktorom je počet hrán veľmi nízky.

Bez ohľadu na to, koľko hrán je v grafe Algoritmus Floyda Warshalla beží na O(V3) krát preto sa najlepšie hodí Husté grafy . V prípade riedkych grafov, Johnsonov algoritmus je vhodnejšia.

  • Ako zistiť negatívny cyklus v grafe pomocou algoritmu Floyd Warshall?
  • Ako sa Floyd-warshallov algoritmus líši od Dijkstrovho algoritmu?
  • Ako sa Floyd-warshallov algoritmus líši od Bellman-Fordovho algoritmu?

Aplikácie Floyd-Warshallovho algoritmu v reálnom svete:

  • V počítačových sieťach sa dá algoritmus použiť na nájdenie najkratšej cesty medzi všetkými pármi uzlov v sieti. Toto sa nazýva ako smerovanie siete .
  • Letová konektivita V leteckom priemysle nájsť najkratšiu cestu medzi letiskami.
  • GIS ( Geografické informačné systémy ) aplikácie často zahŕňajú analýzu priestorových údajov, ako sú cestné siete, s cieľom nájsť najkratšie cesty medzi miestami.
  • Kleeneov algoritmus čo je zovšeobecnenie floyd warshall, možno použiť na nájdenie regulárneho výrazu pre regulárny jazyk.