Rozdeľuj a panuj je algoritmický vzor. V algoritmických metódach je návrhom vziať spor na obrovský vstup, rozdeliť vstup na menšie časti, rozhodnúť o probléme na každom z malých častí a potom zlúčiť po častiach riešenia do globálneho riešenia. Tento mechanizmus riešenia problému sa nazýva Stratégia rozdeľuj a panuj.

Algoritmus Divide and Conquer pozostáva zo sporu pomocou nasledujúcich troch krokov.

Rozdeliťpôvodný problém na množinu podproblémov.dobyť:Riešte každý podproblém jednotlivo, rekurzívne.Kombinovať:Dajte dohromady riešenia čiastkových problémov, aby ste dostali riešenie celého problému.

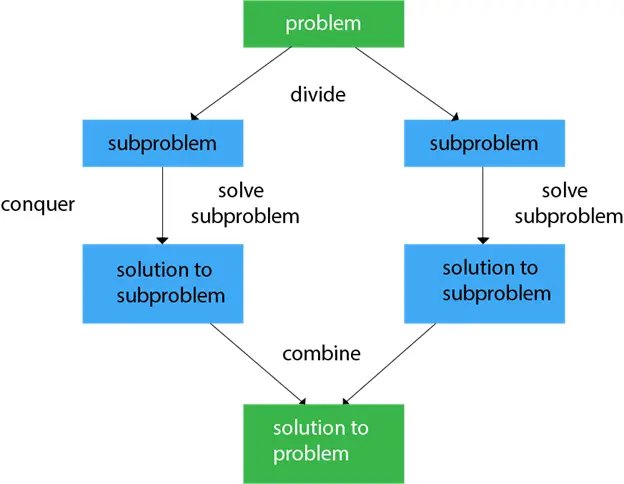
Vo všeobecnosti môžeme sledovať rozdeľ a panuj prístup v trojkrokovom procese.

Príklady: Špecifické počítačové algoritmy sú založené na prístupe Divide & Conquer:

1. Problém maxima a minima
2. Binárne vyhľadávanie
3. Triedenie (zlúčiť triedenie, rýchle triedenie)
4. Hanojská veža.

Základ stratégie rozdeľuj a panuj:

Stratégia Divide & Conquer má dva základné princípy:

1. Relačný vzorec
2. Stav zastavenia

1. Relačný vzorec: Je to vzorec, ktorý vygenerujeme z danej techniky. Po vygenerovaní vzorca aplikujeme stratégiu D&C, t.j. rekurzívne rozbijeme problém a vyriešime rozbité podproblémy.

2. Stav zastavenia: Keď problém prelomíme pomocou stratégie Rozdeľ a panuj, potom musíme vedieť, že na aký čas musíme aplikovať rozdelenie a panuj. Takže stav, kedy je potrebné zastaviť naše rekurzívne kroky D&C, sa nazýva zastavovací stav.

Aplikácie prístupu rozdeľuj a panuj:

Nasledujúce algoritmy sú založené na koncepte techniky rozdeľovania a panovania:

Binárne vyhľadávanie:Binárny vyhľadávací algoritmus je vyhľadávací algoritmus, ktorý sa tiež nazýva polintervalové vyhľadávanie alebo logaritmické vyhľadávanie. Funguje tak, že porovnáva cieľovú hodnotu so stredným prvkom existujúcim v triedenom poli. Po vykonaní porovnania, ak sa hodnota líši, polovica, ktorá nemôže obsahovať cieľ, bude nakoniec vylúčená, po čom bude pokračovať hľadanie na druhej polovici. Opäť zvážime stredný prvok a porovnáme ho s cieľovou hodnotou. Proces sa neustále opakuje, kým sa nedosiahne cieľová hodnota. Ak sme po ukončení hľadania zistili, že druhá polovica je prázdna, potom možno usúdiť, že cieľ sa v poli nenachádza.Rýchle triedenie:Je to najefektívnejší triediaci algoritmus, ktorý je známy aj ako triedenie na výmenu oddielov. Začína sa výberom pivotnej hodnoty z poľa a následným rozdelením zvyšku prvkov poľa do dvoch podpolí. Rozdelenie sa vytvorí porovnaním každého z prvkov s hodnotou pivot. Porovnáva, či má prvok väčšiu alebo menšiu hodnotu ako pivot, a potom rekurzívne triedi polia.Zlúčiť triedenie:Je to triediaci algoritmus, ktorý triedi pole porovnávaním. Začína sa rozdelením poľa na podpole a potom rekurzívne triedi každé z nich. Po dokončení triedenia ich zlúči späť.Najbližšia dvojica bodov:Je to problém výpočtovej geometrie. Tento algoritmus kladie dôraz na zistenie najbližšieho páru bodov v metrickom priestore zadaných n bodov, takže vzdialenosť medzi pármi bodov by mala byť minimálna.Strassenov algoritmus:Je to algoritmus na násobenie matíc, ktorý je pomenovaný po Volkerovi Strassenovi. Ukázalo sa, že je oveľa rýchlejší ako tradičný algoritmus, keď pracuje na veľkých maticách.Cooley-Tukey Fast Fourier Transform (FFT) algoritmus:Algoritmus rýchlej Fourierovej transformácie je pomenovaný po J. W. Cooley a John Turkey. Nasleduje prístup rozdeľuj a panuj a zavádza zložitosť O(nlogn).Algoritmus Karatsuba pre rýchle násobenie:Je to jeden z najrýchlejších algoritmov násobenia tradičnej doby, ktorý vynašiel Anatolij Karatsuba koncom roku 1960 a bol publikovaný v roku 1962. Vynásobí dve n-ciferné čísla tak, že ich zredukuje na maximálne jednociferné.

Výhody rozdeľovania a panovania

• Rozdeľuj a panuj zvyčajne úspešne vyriešiť jeden z najväčších problémov, akým je Hanojská veža, matematický hlavolam. Je náročné riešiť komplikované problémy, o ktorých nemáte žiadnu základnú predstavu, ale s pomocou prístupu rozdeľuj a panuj to znížilo námahu, pretože funguje na rozdelení hlavného problému na dve polovice a následne na ich rekurzívne riešenie. Tento algoritmus je oveľa rýchlejší ako iné algoritmy.
• Efektívne využíva vyrovnávaciu pamäť bez toho, aby zaberala veľa miesta, pretože rieši jednoduché čiastkové problémy vo vyrovnávacej pamäti namiesto prístupu k pomalšej hlavnej pamäti.
• Je zručnejšia ako technika jeho náprotivku Brute Force.
• Keďže tieto algoritmy inhibujú paralelizmus, nezahŕňajú žiadne úpravy a je riešený systémami s paralelným spracovaním.

Nevýhody rozdeľovania a panovania

• Keďže väčšina jeho algoritmov je navrhnutá so začlenením rekurzie, vyžaduje si to vysokú správu pamäte.
• Explicitný zásobník môže nadmerne využívať priestor.
• Môže dokonca dôjsť k zrúteniu systému, ak je rekurzia vykonaná prísne vo väčšej miere ako zásobník prítomný v CPU.