A Počítadlo je zariadenie, ktoré ukladá (a niekedy zobrazuje) počet výskytov konkrétnej udalosti alebo procesu, často vo vzťahu k hodinovému signálu. Počítadlá sa používajú v digitálnej elektronike na účely počítania, môžu počítať konkrétnu udalosť, ktorá sa deje v obvode. Napríklad v počítadle UP počítadlo zvyšuje počet pre každú stúpajúcu hranu hodín. Nielen počítanie, počítadlo môže sledovať určitú sekvenciu založenú na našom dizajne ako akákoľvek náhodná sekvencia 0,1,3,2… .Môžu byť tiež navrhnuté pomocou žabiek. Používajú sa ako frekvenčné deliče, kde sa delí frekvencia daného pulzného priebehu. Počítadlá sú sekvenčný obvod, ktorý počíta počet impulzov môže byť buď v binárnom kóde alebo vo forme BCD. Hlavnými vlastnosťami počítadla sú časovanie, sekvenovanie a počítanie. Počítadlo pracuje v dvoch režimoch
Horný pult
Dolný pult
Protiklasifikácia
Počítadlá sú rozdelené do dvoch kategórií
- Asynchrónne počítadlo
- Synchrónne počítadlo
1. Asynchrónne počítadlo
V asynchrónnom počítadle nepoužívame univerzálne hodiny, iba prvý klopný obvod je poháňaný hlavnými hodinami a hodinový vstup zvyšku nasledujúceho klopného obvodu je poháňaný výstupom predchádzajúcich klopných obvodov. Môžeme to pochopiť nasledujúcim diagramom -
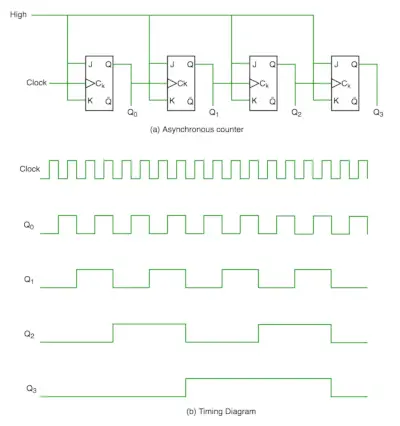
Z časového diagramu je zrejmé, že Q0 sa mení, akonáhle je zaznamenaná stúpajúca hrana hodinového impulzu, Q1 sa mení, keď je zaznamenaná stúpajúca hrana Q0 (pretože Q0 je ako hodinový impulz pre druhý klopný obvod) atď. Týmto spôsobom sa generujú vlnky cez Q0, Q1, Q2, Q3, preto sa tiež nazýva Počítadlo RIPPLE a sériové počítadlo. Počítadlo zvlnenia je kaskádové usporiadanie klopných obvodov, kde výstup jedného klopného obvodu poháňa hodinový vstup nasledujúceho klopného obvodu.
2. Synchrónne počítadlo
Na rozdiel od asynchrónneho počítadla má synchrónne počítadlo jedny globálne hodiny, ktoré riadia každý klopný obvod, takže výstup sa mení paralelne. Jednou z výhod synchrónneho počítadla oproti asynchrónnemu počítadlu je, že môže pracovať na vyššej frekvencii ako asynchrónne počítadlo, pretože nemá kumulatívne oneskorenie, pretože každý klopný obvod má rovnaké hodiny. Nazýva sa tiež paralelné počítadlo.
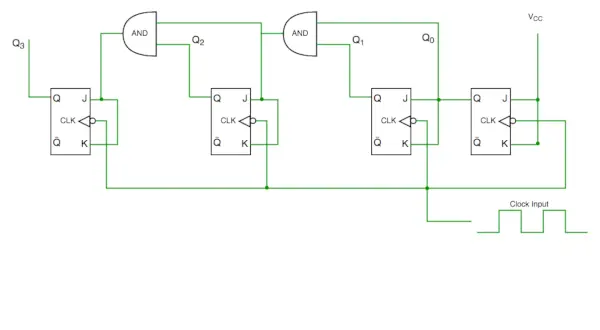
Synchrónny obvod počítadla
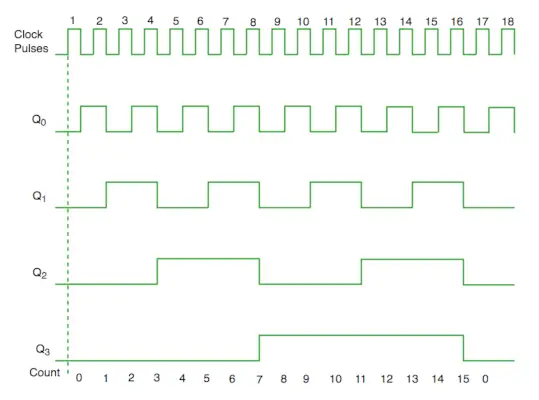
Časový diagram synchrónne počítadlo
Zo schémy zapojenia vidíme, že bit Q0 dáva odozvu na každú zostupnú hranu hodín, zatiaľ čo Q1 je závislý na Q0, Q2 je závislý na Q1 a Q0, Q3 je závislý na Q2, Q1 a Q0.
Počítadlo desaťročí
Počítadlo desaťročí počíta desať rôznych stavov a potom sa resetuje do počiatočných stavov. Jednoduché počítadlo dekád bude počítať od 0 do 9, ale môžeme vytvoriť aj počítadlá dekád, ktoré môžu prejsť ľubovoľnými desiatimi stavmi medzi 0 až 15 (pre 4 bitové počítadlo).
| Hodinový pulz | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 0 |
Tabuľka pravdy pre jednoduché počítadlo desaťročí
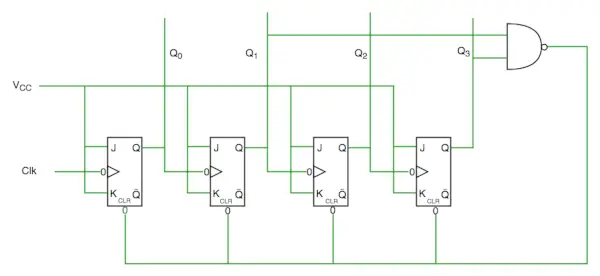
Schéma zapojenia počítadla desaťročí
Zo schémy zapojenia vidíme, že sme použili nand gate pre Q3 a Q1 a priviedli sme to na vyčistenie vstupného riadku, pretože binárne znázornenie 10 je —
1010
A vidíme, že Q3 a Q1 sú tu 1, ak dáme NAND z týchto dvoch bitov na vymazanie vstupu, potom sa počítadlo vymaže na 10 a začne znova od začiatku.
Dôležitý bod : Počet žabiek použitých v počítadle je vždy väčší ako rovný ( log2n ) kde n=počet stavov v čítači.
Niektoré z predchádzajúcich rokov vstupné otázky na pultoch
Q1. Zvážte čiastočnú implementáciu 2-bitového počítadla pomocou T klopných obvodov podľa sekvencie 0-2-3-1-0, ako je uvedené nižšie
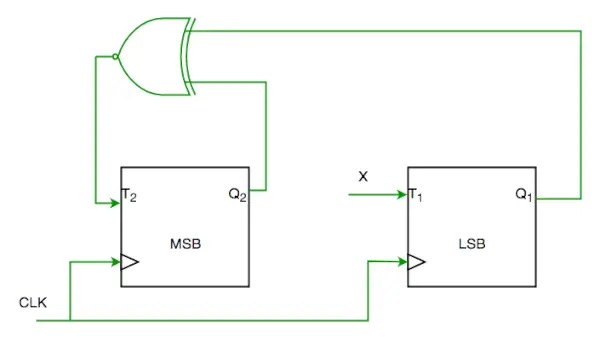
Na dokončenie obvodu by mal byť vstup X
(A) Q2?
(B) Q2 + Q1
(C) (Q1 ? Q2)“
(D) Q1 ? Q2 (GATE-CS-2004)
Riešenie:
Z okruhu vidíme
T1=XQ1'+X'Q1—-(1)
A
T2=(Q2 ? Q1)'—-(2)
A POŽADOVANÝ VÝSTUP JE 00->10->11->01->00
TAK BY MAL BYŤ X Q1Q2’+Q1’Q2 SPOKOJNÉ 1 A 2.
TAKŽE ANS JE (D) ČASŤOU.
Q2. Funkcie riadiaceho signálu 4-bitového binárneho počítadla sú uvedené nižšie (kde X je jedno)
Počítadlo je pripojené nasledovne:
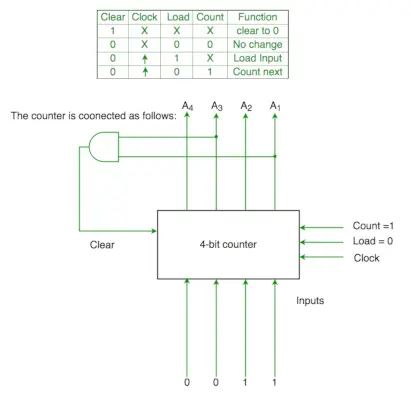
Predpokladajme, že oneskorenia počítadla a brány sú zanedbateľné. Ak počítadlo začína na 0, potom cyklicky prechádza nasledujúcou sekvenciou:
(A) 0,3,4
(B) 0,3,4,5
(C) 0,1,2,3,4
(D) 0,1,2,3,4,5 (GATE-CS-2007)
Riešenie:
Na začiatku A1 A2 A3 A4 = 0000
Clr = A1 a A3
Takže keď sú A1 a A3 obidva 1, opäť sa dostane na 0000
Preto 0000(začiatok) -> 0001(A1 a A3=0)->0010 (A1 a A3=0) -> 0011(A1 a A3=0) -> 0100 ( A1 a A3 = 1 )[ jasná podmienka splnená] -> 0000 (init.), takže prechádza cez 0->1->2->3->4
Ans je časť (C).
kat timpf hmotnosť
Kvíz o digitálnej logike
Článok prispel Anuj Batham,
