Predpoklad – Data Mining , miera podobnosti sa vzťahuje na vzdialenosť s dimenziami reprezentujúcimi vlastnosti dátového objektu v množine údajov. Ak je táto vzdialenosť menšia, bude existovať vysoký stupeň podobnosti, ale ak je vzdialenosť veľká, bude existovať nízky stupeň podobnosti. Niektoré z populárnych mier podobnosti sú –

1. Euklidovská vzdialenosť.
2. Vzdialenosť Manhattan.
3. Podobnosť Jaccarda.
4. Minkowského vzdialenosť.
5. Kosínusová podobnosť.

Kosínusová podobnosť je metrika, ktorá pomáha pri určovaní toho, nakoľko podobné sú dátové objekty bez ohľadu na ich veľkosť. Podobnosť medzi dvoma vetami môžeme merať v Pythone pomocou kosínovej podobnosti. V kosínusovej podobnosti sa s dátovými objektmi v množine údajov zaobchádza ako s vektorom. Vzorec na nájdenie kosínusovej podobnosti medzi dvoma vektormi je -

(x, y) = x . y / ||x||  ||y||>

kde,

X . y = súčin (bodka) vektorov „x“ a „y“.||x|| a ||a|| = dĺžka (veľkosť) dvoch vektorov „x“ a „y“.||x|| ||a|| = pravidelný súčin dvoch vektorov „x“ a „y“.

Príklad: Zvážte príklad, aby ste našli podobnosť medzi dvoma vektormi - 'X' a 'a' pomocou kosínusovej podobnosti. Vektor „x“ má hodnoty, x = { 3, 2, 0, 5 } Vektor „y“ má hodnoty, y = { 1, 0, 0, 0 } Vzorec na výpočet kosínusovej podobnosti je: (x, y) = x. y / ||x|| ||a||

x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3 ||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16 ||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1 ∴ (x, y) = 3 / (6.16 * 1) = 0.49>

Nepodobnosť medzi dvoma vektormi „x“ a „y“ je daná –

∴ (x, y) = 1 - (x, y) = 1 - 0.49 = 0.51>

• Kosínusová podobnosť medzi dvoma vektormi sa meria v „θ“.
• Ak θ = 0°, vektory „x“ a „y“ sa prekrývajú, čím sa dokazuje, že sú podobné.
• Ak θ = 90°, vektory „x“ a „y“ sú odlišné.

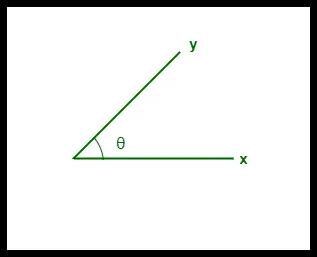
Kosínusová podobnosť medzi dvoma vektormi

Výhody:

• Kosínusová podobnosť je výhodná, pretože aj keď sú dva podobné dátové objekty vzdialené od seba o euklidovskú vzdialenosť kvôli veľkosti, stále môžu mať medzi sebou menší uhol. Čím menší uhol, tým väčšia podobnosť.
• Pri vykresľovaní do viacrozmerného priestoru kosínusová podobnosť zachytáva orientáciu (uhol) dátových objektov a nie veľkosť.