Vedro triediť je technika triedenia, ktorá zahŕňa rozdelenie prvkov do rôznych skupín alebo vedier. Tieto vedrá sú tvorené rovnomerným rozložením prvkov. Po rozdelení prvkov do segmentov je možné ich triediť pomocou akéhokoľvek iného triediaceho algoritmu. Nakoniec sa zoradené prvky zhromaždia usporiadaným spôsobom.
Algoritmus triedenia segmentov:
Vytvorte n prázdne vedrá (alebo zoznamy) a pre každý prvok poľa arr[i] vykonajte nasledujúce.
- Vložte arr[i] do bucket[n*array[i]]
- Zoraďte jednotlivé segmenty pomocou zoradenia vložením.
- Spojiť všetky zoradené vedrá.
Ako funguje Bucket Sort?
Ak chcete použiť triedenie segmentov na vstupné pole [0,78, 0,17, 0,39, 0,26, 0,72, 0,94, 0,21, 0,12, 0,23, 0,68] , postupujeme podľa týchto krokov:
Krok 1: Vytvorte pole veľkosti 10, kde každý slot predstavuje vedro.
10 ml až oz

Vytváranie vedier na triedenie
Krok 2: Vložte prvky do segmentov zo vstupného poľa na základe ich rozsahu.
ako zatvoriť režim vývojára
Vkladanie prvkov do vedier:
- Vezmite každý prvok zo vstupného poľa.
- Vynásobte prvok veľkosťou poľa vedierka (v tomto prípade 10). Napríklad pre prvok 0,23 dostaneme 0,23 * 10 = 2,3.
- Výsledok preveďte na celé číslo, čím získame index segmentu. V tomto prípade sa 2,3 prevedie na celé číslo 2.
- Vložte prvok do vedra zodpovedajúceho vypočítanému indexu.
- Opakujte tieto kroky pre všetky prvky vo vstupnom poli.
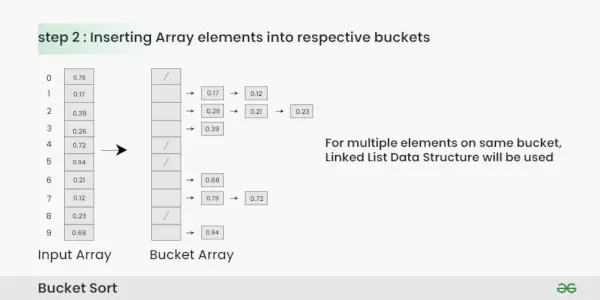
Vkladanie prvkov Array do príslušných vedier
Krok 3: Zoraďte prvky v každom vedre. V tomto príklade používame rýchle triedenie (alebo akýkoľvek stabilný algoritmus triedenia) na triedenie prvkov v každom segmente.
Zoradenie prvkov v každom vedre:
- Použite stabilný algoritmus triedenia (napr. Bubble Sort, Merge Sort) na zoradenie prvkov v každom segmente.
- Prvky v každom segmente sú teraz zoradené.
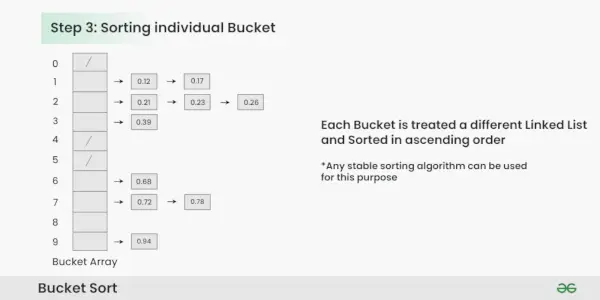
Triedenie jednotlivých vedier
Krok 4: Zhromaždite prvky z každého vedra a vložte ich späť do pôvodného poľa.
Zhromažďovanie prvkov z každého vedra:
- Iterujte cez každý vedro v poradí.
- Vložte každý jednotlivý prvok z vedra do pôvodného poľa.
- Po skopírovaní prvku sa prvok odstráni z vedra.
- Tento postup opakujte pre všetky vedrá, kým nezozbierate všetky prvky.
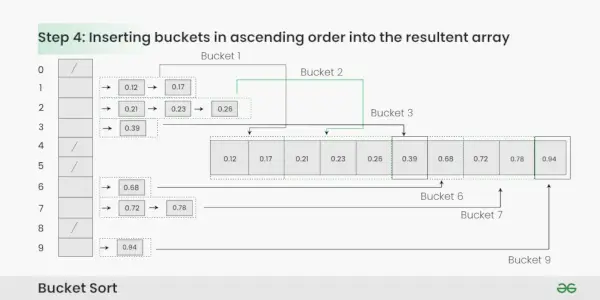
Vkladanie vedierok vo vzostupnom poradí do výsledného poľa
príklady programovania v pythone
Krok 5: Pôvodné pole teraz obsahuje zoradené prvky.
Konečné zoradené pole pomocou triedenia segmentov pre daný vstup je [0,12, 0,17, 0,21, 0,23, 0,26, 0,39, 0,68, 0,72, 0,78, 0,94].
1 z 1 000,00

Vráťte triedené pole
Implementácia algoritmu triedenia segmentov:
Nižšie je uvedená implementácia triedenia segmentov:
C++ #include #include using namespace std; // Insertion sort function to sort individual buckets void insertionSort(vector& vedro) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && bucket[j]> key) { bucket[j + 1] = bucket[j]; j--; } vedro[j + 1] = kľúč; } } // Funkcia na triedenie arr[] veľkosti n pomocou bucket sort void bucketSort(float arr[], int n) { // 1) Vytvorenie n prázdnych bucketovb[n]; // 2) Vložte prvky poľa do rôznych segmentov pre (int i = 0; i< n; i++) { int bi = n * arr[i]; b[bi].push_back(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(b[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < b[i].size(); j++) { arr[index++] = b[i][j]; } } } // Driver program to test above function int main() { float arr[] = {0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434}; int n = sizeof(arr) / sizeof(arr[0]); bucketSort(arr, n); cout << 'Sorted array is
'; for (int i = 0; i < n; i++) { cout << arr[i] << ' '; } return 0; }>
Java import java.util.ArrayList; import java.util.List; public class Main { // Insertion sort function to sort individual buckets public static void insertionSort(Listvedro) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket.get(i); int j = i - 1; while (j>= 0 && bucket.get(j)> key) { bucket.set(j + 1, bucket.get(j)); j--; } bucket.set(j + 1, kľúč); } } // Funkcia na triedenie arr[] veľkosti n pomocou bucket sort public static void bucketSort(float[] arr) { int n = arr.length; // 1) Vytvorte n prázdnych bucketov List[] buckets = new ArrayList[n]; pre (int i = 0; i< n; i++) { buckets[i] = new ArrayList(); } // 2) Put array elements in different buckets for (int i = 0; i < n; i++) { int bi = (int) (n * arr[i]); buckets[bi].add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].size(); j++) { arr[index++] = buckets[i].get(j); } } } // Driver program to test above function public static void main(String[] args) { float[] arr = {0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f}; bucketSort(arr); System.out.println('Sorted array is:'); for (float num : arr) { System.out.print(num + ' '); } } }> Python def insertion_sort(bucket): for i in range(1, len(bucket)): key = bucket[i] j = i - 1 while j>= 0 a bucket[j]> kľúč: bucket[j + 1] = bucket[j] j -= 1 bucket[j + 1] = key def bucket_sort(arr): n = len(arr) buckets = [[] for _ in range(n)] # Umiestnite prvky poľa do rôznych segmentov pre num in arr: bi = int(n * num) buckets[bi].append(num) # Zoraďte jednotlivé segmenty pomocou zoradenia vloženia pre segment v segmentoch: insertion_sort (vedro) # Zreťaziť všetky segmenty do arr[] index = 0 pre segment v segmente: pre num in bucket: arr[index] = num index += 1 arr = [0,897, 0,565, 0,656, 0,1234, 0,663, 0,663] segment_sort (arr) print('Sorted array is:') print(' '.join(map(str, arr)))> C# using System; using System.Collections.Generic; class Program { // Insertion sort function to sort individual buckets static void InsertionSort(Listvedro) { for (int i = 1; i< bucket.Count; ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && bucket[j]> key) { bucket[j + 1] = bucket[j]; j--; } vedro[j + 1] = kľúč; } } // Funkcia na triedenie arr[] veľkosti n pomocou bucket sort static void BucketSort(float[] arr) { int n = arr.Length; // 1) Vytvorte n prázdnych bucketov List[] vedrá = nový zoznam[n]; pre (int i = 0; i< n; i++) { buckets[i] = new List(); } // 2) Vložte prvky poľa do rôznych segmentov pre (int i = 0; i< n; i++) { int bi = (int)(n * arr[i]); buckets[bi].Add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { InsertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].Count; j++) { arr[index++] = buckets[i][j]; } } } // Driver program to test above function static void Main(string[] args) { float[] arr = { 0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f }; BucketSort(arr); Console.WriteLine('Sorted array is:'); foreach (float num in arr) { Console.Write(num + ' '); } } }> JavaScript function insertionSort(bucket) { for (let i = 1; i < bucket.length; ++i) { let key = bucket[i]; let j = i - 1; while (j>= 0 && bucket[j]> key) { bucket[j + 1] = bucket[j]; j--; } vedro[j + 1] = kľúč; } } function bucketSort(arr) { nech n = arr.length; let buckets = Array.from({dĺžka: n}, () => []); // Vložte prvky poľa do rôznych segmentov pre (nech i = 0; i< n; i++) { let bi = Math.floor(n * arr[i]); buckets[bi].push(arr[i]); } // Sort individual buckets using insertion sort for (let i = 0; i < n; i++) { insertionSort(buckets[i]); } // Concatenate all buckets into arr[] let index = 0; for (let i = 0; i < n; i++) { for (let j = 0; j < buckets[i].length; j++) { arr[index++] = buckets[i][j]; } } } let arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434]; bucketSort(arr); console.log('Sorted array is:'); console.log(arr.join(' '));> Výkon
Sorted array is 0.1234 0.3434 0.565 0.656 0.665 0.897>
Analýza zložitosti algoritmu triedenia segmentov:
Časová zložitosť: O(n2),
- Ak predpokladáme, že vloženie do vedra trvá O(1) čas, potom kroky 1 a 2 vyššie uvedeného algoritmu jednoznačne trvajú O(n) čas.
- O(1) je ľahko možné, ak na reprezentáciu vedra použijeme prepojený zoznam.
- Krok 4 tiež trvá O(n) čas, pretože vo všetkých segmentoch bude n položiek.
- Hlavným krokom analýzy je krok 3. Tento krok tiež trvá v priemere O(n) čas, ak sú všetky čísla rovnomerne rozdelené.
Pomocný priestor: O(n+k)
