Rýchlosť je jednoducho taká, ako poznáte mieru toho, ako rýchlo alebo pomaly sa objekt pohybuje, napríklad ako rýchlo jazdíte autom. Teraz tu hovoríme o špecifickom type rýchlosti. Uhlová rýchlosť je len typ rýchlosti, ale tu sa telo musí pohybovať po kruhovej dráhe.

Vzorec uhlovej rýchlosti

Uhlová rýchlosť je definovaná ako rýchlosť zmeny uhlového posunu, čo je uhol, ktorý prejde teleso pozdĺž kruhovej dráhy. Uhlová rýchlosť je vypočítaná ako počet otáčok/otáčok uskutočnených telesom za čas. Uhlová rýchlosť sa označuje gréckym písmenom „ω“ známym ako Omega. Jednotkou SI uhlovej rýchlosti je rad/s.

Uhlová rýchlosť sa vypočíta pomocou dvoch rôznych vzorcov,

ω = θ/t ω = v/r

Odvodenie vzorca

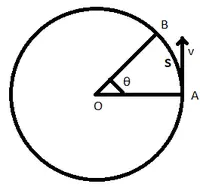
Uvažujme teleso pohybujúce sa po kruhovej dráhe s polomerom r zobrazeným vyššie s lineárnou rýchlosťou v. Predpokladajme, že sa teleso pohybuje z bodu A do B, pričom prekoná vzdialenosť s cez kruhový oblúk a prekoná uhol θ v časovom období t.

Kruhová dráha pokrytá telom

Ako je známe, uhlová rýchlosť je rýchlosť zmeny posunutia – uhlová rýchlosť, ω = θ/t

Takže vzorec pre uhlovú rýchlosť je ω = θ/t .

Ďalší vzorec pre uhlovú rýchlosť

Napriek vyššie uvedenému vzorcu existuje ďalší a viac používaný vzorec na výpočet uhlovej rýchlosti z pohľadu súťažných skúšok.

Ako ω = θ/t ⇢ (1)

Teraz vieme, že vzdialenosť presunutá cez oblúk kružnice sa rovná polomeru krát prejdený uhol. takže,

s = r8

=> θ = s/r ⇢ (2)

IMMS hry s Androidom

Od (1) a (2),

ω = s/(rt) ⇢ (3)

Aj zo všeobecného chápania lineárnych rýchlostí,

v = s/t ⇢ (4)

Od (3) a (4),

ω = v/r

Ukážkové problémy

Otázka 1: Uvažujme teleso pohybujúce sa po kruhovej dráhe s polomerom 5 m. Polovičnú otáčku pokryje za 5 s. Vypočítajte jeho uhlovú rýchlosť.

Riešenie:

Pri polovičnej otáčke je uhol prejdenia 180 stupňov. V radiánoch sa rovná π radiánom.

ω = θ/t

=> ω = π/5 = 0,628 rad/s

Otázka 2: Koleso automobilu s polomerom 2 m sa otáča lineárnou rýchlosťou 10 m/s. Vypočítajte jej uhlovú rýchlosť.

Riešenie:

ω = v/r

ω = 10/2

= 5 rad/s

Otázka 3: Uvažujme pretekárske auto pohybujúce sa po kruhovej dráhe rýchlosťou 18 km/h a polomerom dráhy 0,2 m. Vypočítajte uhlovú rýchlosť auta.

Riešenie:

v = 18 km/h = 5 m/s

r = 0,2 m

ω = v/r

= 5/0,2

= 25 rad/s

Otázka 4: Automobil sa pohybuje po kruhovej dráhe s polomerom 2 m uhlovou rýchlosťou 2 rad/s. Vypočítajte uhol v stupňoch, o ktorý sa auto pohne za 2 s.

Riešenie:

Vzhľadom na to, w = 2 rad/s a t = 2 s

Keďže ω = θ/t => θ = ωt

=> θ = (2 × 2) = 4 rad

V stupňoch θ = 4 × (180/π) = 229,18 stupňa

Otázka 5: Koľko otáčok vykonalo teleso pohybujúce sa po kruhovej dráhe s uhlovou rýchlosťou 7π rad/s za 0,5 s?

Riešenie:

Dané ω = 7π rad/s a t = 0,5 s

Keďže ω = θ/t => θ = ωt

θ = (7π × 0,5) = 3,5π

V 2π rad sú pokryté otáčky 1

=> V 1 rad je pokrytá otáčka (1/2π)

=> V 3,5π rad, otáčky = 3,5π/2π = 1,75 otáčky

Telo teda vykoná 1 kompletnú otáčku a 3/4 ďalšej otáčky v časovom úseku 0,5 s.

Otázka 6: Aká bude uhlová rýchlosť telesa pohybujúceho sa po kruhovej dráhe s polomerom 2 m, ktorá pokrýva 4 m oblúka dĺžky 5 s.

Riešenie:

Dané s = 4 m, r = 2 m, t = 5 s

Pomocou vzorca s = rθ => θ = s/r

θ = 4/2 = 2 rad

Pretože ω = θ/t

komponenty robota

=> ω = 2/5 = 0,4 rad/s