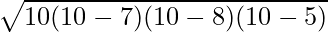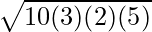Ostrý uhlový trojuholník je trojuholník, v ktorom sú všetky uhly trojuholníkov ostré. Trojuholník môže mať iba jeden uhol ako pravý alebo tupý uhol kvôli vlastnosti súčtu uhla trojuholníka. Preto trojuholník, ktorý má všetky tri uhly ako ostré uhly, t. j. uhly s hodnotou menšou ako 90 stupňov, sa nazýva trojuholník s ostrým uhlom.

Na základe typov vnútorných uhlov trojuholníka možno trojuholník rozdeliť do troch kategórií, trojuholníky s ostrým uhlom, trojuholníky s tupým uhlom a pravouhlé trojuholníky. Teraz sa v tomto článku dozvieme viac o trojuholníkoch s ostrým uhlom, ich typoch, vlastnostiach a ďalších.

Čo je to trojuholník s ostrým uhlom?

An trojuholník s ostrým uhlom je definovaný ako trojuholník, ktorého všetky tri vnútorné uhly sú ostré, t.j. ich hodnota je medzi 0° a 90°. V závislosti od typu trojuholníka môžu byť dĺžky strán trojuholníka s ostrým uhlom rovnaké alebo nerovnaké. Ostrouhlý trojuholník tiež sleduje vlastnosť súčtu uhla trojuholníka.

Obrázok uvedený nižšie je trojuholník s ostrým uhlom, ktorého vnútorné uhly sú 45°, 35° a 80°. Keďže tri vnútorné uhly sú menšie ako 90°, daný trojuholník je trojuholník s ostrým uhlom.

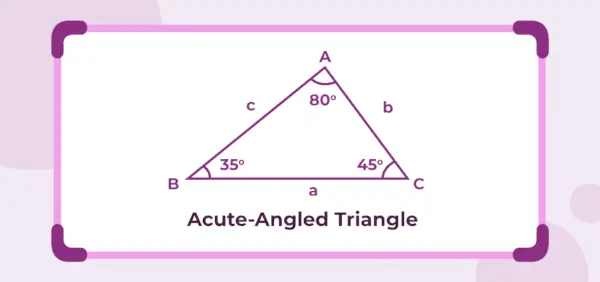
Definícia trojuholníka s ostrým uhlom

Trojuholníky s ostrým uhlom sú definované, ako naznačuje názov, ako trojuholníky, v ktorých všetky tri uhly trojuholníka sú ostré uhly. Strana v trojuholníkoch s ostrým uhlom môže byť rovnaká alebo nerovná a na základe toho sa ďalej delia na tri časti, o ktorých sa hovorí v článku nižšie,

Typy trojuholníkov s ostrým uhlom

Trojuholníky s ostrým uhlom sú rozdelené do troch typov v závislosti od dĺžky strán trojuholníkov,

• Rovnostranný akútny trojuholník
• Rovnoramenný akútny trojuholník
• Scalene Acute Triangle

Teraz sa o nich dozvieme podrobnejšie.

Rovnostranný akútny trojuholník

Rovnostranný ostrý trojuholník, tiež nazývaný rovnostranný trojuholník, je trojuholník, v ktorom sú všetky uhly ostré a všetky uhly sú rovnaké, rovnako aj strana rovnostranných ostrých trojuholníkov. Každý uhol rovnostranného ostrého trojuholníka meria vždy 60°.

Rovnoramenný akútny trojuholník

Rovnoramenný ostrý trojuholník je trojuholník, v ktorom sú všetky uhly ostré a dva ľubovoľné uhly trojuholníka a strana zodpovedajúca týmto uhlom sú rovnaké. To znamená, že v rovnoramennom ostrom trojuholníku máme dve strany a ich zodpovedajúce uhly sú rovnaké.

Scalene Acute Triangle

Skalnatý ostrý trojuholník je trojuholník, v ktorom sú všetky uhly ostré a žiadne dva uhly a žiadne dve strany nie sú rovnaké. To znamená, že v miernom ostrom trojuholníku nemáme rovnaké strany ani uhly.

Vlastnosti trojuholníka s ostrým uhlom

Nasledujú niektoré dôležité vlastnosti trojuholníka s ostrým uhlom,

• Vnútorné uhly trojuholníka s ostrým uhlom sú ostré uhly, t. j. uhly sú väčšie ako 0°, ale menšie ako 90°.
• Vnútorné uhly trojuholníkov s ostrým uhlom sledujú vlastnosť súčtu uhlov, t. j. súčet uhlov trojuholníka s ostrým uhlom je 180°.
• Rovnostranný trojuholník je vždy trojuholník s ostrým uhlom, pretože každý vnútorný uhol rovnostranného trojuholníka meria 60°.
• Trojuholník nemôže byť súčasne pravouhlým trojuholníkom a trojuholníkom s ostrým uhlom.
• Trojuholník nemôže byť súčasne trojuholníkom s ostrým uhlom a trojuholníkom s tupouhlým uhlom.
• V trojuholníku s ostrým uhlom je strana opačná k najmenšiemu uhlu najmenšia a platí aj jej prevrátená strana.
• Podobne strana oproti najväčšiemu uhlu je najväčšia a platí to aj naopak.

Vzorce trojuholníka s ostrým uhlom

Plocha a obvod sú dva základné vzorce trojuholníka s ostrým uhlom, o ktorých sa hovorí nižšie.

Obvod trojuholníka s ostrým uhlom

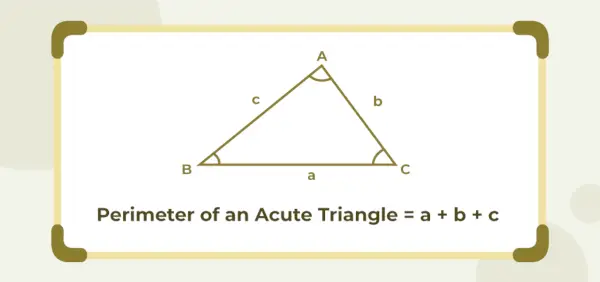
Obvod trojuholníka s ostrým uhlom sa rovná súčtu dĺžok jeho troch strán. Ak a, b a c sú dĺžky strán trojuholníka s ostrým uhlom, potom je jeho obvod daný ako jednotky (a + b + c).

Obvod trojuholníka s ostrým uhlom = (a + b + c) jednotiek

Kde a , b , a c sú dĺžky strán trojuholníka.

Čítaj viac, Obvod trojuholníka

Oblasť trojuholníka s ostrým uhlom

Plocha trojuholníka je definovaná ako celkový priestor ohraničený tromi stranami akéhokoľvek trojuholníka v dvojrozmernej rovine.

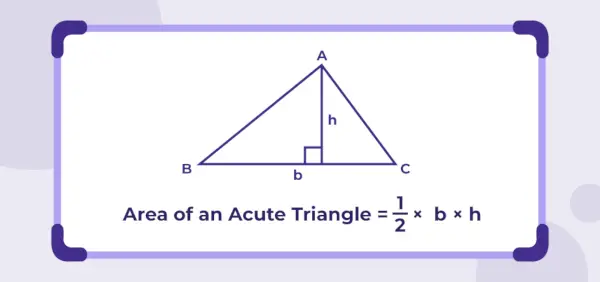
Plocha trojuholníka s ostrým uhlom = ½ × b × h

Kde,

b je základná dĺžka ah je výška trojuholníka.

Čítaj viac, Oblasť trojuholníka

Akútna oblasť trojuholníka podľa Heronovho vzorca

Ak sú uvedené tri dĺžky strán trojuholníka s ostrým uhlom, potom sa jeho plocha môže vypočítať pomocou Heronovho vzorca.

Oblasť trojuholníka s ostrým uhlom =

Kde,

s je polobvod a s = (a + b + c)/2 , ty , b , a c sú dĺžky strán trojuholníka.

Čítaj viac, Heronova formula

Dôležité terminológie trojuholníka

Rôzne terminológie súvisiace s trojuholníkom s ostrým uhlom sú:

Okolo centra

Stred kružnice, ktorá prechádza tromi vrcholmi trojuholníka, sa nazýva stred trojuholníka. Vypočíta sa ako priesečník kolmice. V prípade trojuholníka s ostrým uhlom leží stred vždy vo vnútri trojuholníka.

Incenter

Stred kruhu, ktorý sa dotýka troch strán trojuholníka, sa nazýva stred trojuholníka. Vypočíta sa ako priesečník uhlovej osy. V prípade trojuholníka s ostrým uhlom stred vždy leží vo vnútri trojuholníka.

Centroid

Priesečník stredov trojuholníka sa nazýva ťažisko trojuholníka. V prípade trojuholníka s ostrým uhlom leží ťažisko trojuholníka vždy vo vnútri trojuholníka.

Ortocentrum

Priesečník výšky trojuholníka sa nazýva ortocentrum trojuholníka. V prípade trojuholníka s ostrým uhlom leží ortocentrum trojuholníka vždy vo vnútri trojuholníka.

Vyriešené príklady na ostrom uhlovom trojuholníku

Príklad 1: Ktorý z nasledujúcich uhlov môže vytvoriť trojuholník s ostrým uhlom?

a) 65°, 75°, 50° b) 95°, 40°, 45° c) 70°, 40°, 70° d) 90°, 45°, 45°

Riešenie:

Vieme, že všetky uhly v trojuholníku s ostrým uhlom sú ostré uhly, čo je ich miera menšia ako 90 stupňov.

Tiež sledujú vlastnosť súčtu uhlov trojuholníka, t. j. všetky ich uhly tvoria súčet až 180 stupňov.

a) 65°, 75°, 50°

Tu sú všetky uhly ostré uhly, ale nesleduje to vlastnosť súčtu uhlov, takže trojuholník nie je možný.

65°+ 75°+ 50° = 190° (trojuholník nie je možný)

b) 95°, 40°, 45°

Tu je trojuholník možný, pretože sleduje súčet uhlov trojuholníka, t.j.

95°+ 40°+ 45° = 180

Ale pri pozorovaní uhlov trojuholníka sme našli tupý uhol 95°. Preto trojuholník nie je trojuholník s ostrým uhlom.

c) 70°, 40°, 70°

Tu je trojuholník možný, pretože sleduje súčet uhlov trojuholníka, t.j.

70°+ 40°+ 70° = 180

A pri pozorovaní uhlov trojuholníka sme zistili, že všetky uhly sú ostré. Preto je trojuholník trojuholníkom s ostrým uhlom.

d) 90°, 45°, 45°

Tu je trojuholník možný, pretože sleduje súčet uhlov trojuholníka, t.j.

90°+ 45°+ 45° = 180

Ale pri pozorovaní uhlov trojuholníka sme našli pravý uhol 90°. Preto trojuholník nie je trojuholník s ostrým uhlom.

Príklad 2: Nájdite obvod ostrého trojuholníka XYZ, ktorého strany sú XY = 8 jednotiek, YZ = 5 jednotiek a XZ = 9 jednotiek.

Riešenie:

Vzhľadom na to,

Strany akútneho - uhlového trojuholníka,

• XY(x) = 8 jednotiek
• YZ(y) = 5 jednotiek
• XZ(z) = 9 jednotiek

My to vieme,

Obvod trojuholníka s ostrým uhlom (P) = x + y + z

⇒ P = (8 + 5 + 9) jednotiek

⇒ P = 22 jednotiek

Obvod trojuholníka s ostrým uhlom je teda 22 jednotiek.

Príklad 3: Nájdite obsah ostrého trojuholníka, ktorého výška je 12 jednotiek a základňa je 15 jednotiek.

Riešenie:

Vzhľadom na to,

• Výška trojuholníka (h) = 12 jednotiek
• Dĺžka základne trojuholníka (b) = 15 jednotiek

My to vieme,

Plocha trojuholníka (A) = ½ × b × h

⇒ A = ½ × 12 × 15

⇒ A = ½ × 180

aktualizácia z join sql

⇒ A = 90 štvorcových jednotiek.

Plocha daného ostrého trojuholníka je teda 90 štvorcových jednotiek.

Príklad 4: Nájdite obsah ostrého trojuholníka, ktorého strany sú AB = 5 cm, BC = 7 cm a AC = 8 cm.

Riešenie:

Vzhľadom na to,

Strany akútneho - uhlového trojuholníka,

• AB = c = 5 jednotiek
• BC = a = 7 jednotiek
• AC = b = 8 jednotiek

My to vieme,

Oblasť trojuholníka =

⇒ A =

⇒ A =

⇒ A = √(300) cm2

⇒ A = 10√3 cm2

Plocha daného ostrého trojuholníka je teda 10√3 cm2.

Časté otázky o akútnom uhlovom trojuholníku

Q1: Čo sú to akútne uhly?

odpoveď:

Uhol v rozsahu od 0° do 90° sa nazýva ostré uhly. To znamená, že minimálna hodnota ostrého uhla je väčšia ako 0° a maximálna hodnota ostrého uhla je väčšia ako 90°.

Q2: Čo je to trojuholník s ostrým uhlom?

odpoveď:

Ostrouhlý trojuholník je trojuholník, ktorého všetky tri vnútorné uhly sú ostré uhly, t.j. hodnota uhla je medzi 0° a 90°.

Otázka 3: Je rovnostranný trojuholník vždy trojuholníkom s ostrým uhlom?

odpoveď:

Áno, rovnostranný trojuholník je vždy trojuholník s ostrým uhlom. Ostrouhlé trojuholníky sú uhly, ktorých všetky uhly majú ostré uhly a v rovnostrannom trojuholníku sú všetky uhly 60°, t.j. ostré uhly. Preto je rovnostranný trojuholník vždy trojuholník s ostrým uhlom.

Otázka 4: Aké sú rôzne typy trojuholníkov s ostrým uhlom?

odpoveď:

Trojuholníky s ostrým uhlom sú rozdelené do troch typov, ktoré sú:

• Scalene Acute Triangle
• Rovnoramenný akútny trojuholník
• Rovnostranný akútny trojuholník

Q5: Ako zistiť, či je trojuholník trojuholníkom s ostrým uhlom?

odpoveď:

Trojuholník, ktorého vnútorné uhly sú menšie ako 90°, t.j. všetky vnútorné uhly sú ostré, sa nazýva trojuholník s ostrým uhlom. Či je trojuholník ostrý, môžeme skontrolovať jednoduchým pozorovaním uhlov trojuholníka.