Zrýchlenie je zmena rýchlosti s časom. V reálnom živote sa zrýchlenie tiež mení s časom. Napríklad cestujete z jedného mesta do druhého po ceste. Potom v tomto prípade zrýchlite viac v prípade prázdnej cesty a zrýchlite dole v prípade premávky. Túto zmenu zrýchlenia možno pozorovať vynesením zrýchlenia proti času do grafu. Toto sa nazýva graf času zrýchlenia. V tomto článku sa podrobne dozvieme o časovom grafe zrýchlenia a na jeho základe budeme riešiť problémy.

modely strojového učenia

Čo je graf zrýchlenia?

Graf zrýchlenia-čas sa používa na znázornenie vzťahu medzi zrýchlenie a čas, kde zrýchlenie je nezávislá premenná vynesená na osi Y a čas je závislá premenná vynesená na osi X. Získava sa, keď sa získané údaje o zrýchlení a čase vynesú do pravouhlého grafu pri štúdiu pohybu telesa. Zmenu rýchlosti v danom časovom intervale môžeme určiť pomocou grafu zrýchlenie-čas. Určením plochy pod krivkou grafu zrýchlenia a času môžeme nájsť zmenu rýchlosti pohybujúceho sa objektu za určitú dobu.

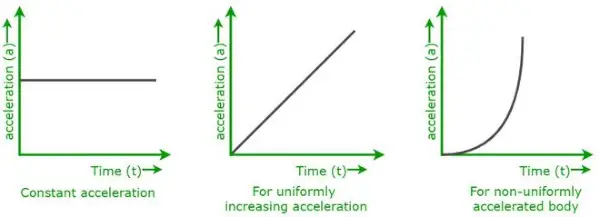
Vyššie uvedené grafy sú grafy zrýchlenia a času pre rôzne typy pohybu tela.

1. Keď sa telo pohybuje konštantným zrýchlením,
2. Keď sa teleso pohybuje rovnomerne so zvyšujúcim sa zrýchlením.
3. Keď sa teleso pohybuje nerovnomerne s premenlivým zrýchlením.

Závery

Nasledujú body odvodené z grafov zrýchlenia-čas.

• Sklon grafu zrýchlenia-čas je △a/△t.
• Oblasť pod grafom zrýchlenia-čas predstavuje zmenu rýchlosti.

nech,

△v byť zmenou rýchlosti,

△a byť zmenou v zrýchlení,

△t byť zmenou v čase.

teraz plocha pod krivkou = △v

Vieme, že zrýchlenie telesa sa označuje ako rýchlosť zmeny rýchlosti v danom časovom období.

takže,

△a = △v/△t

Teraz, vynásobením s △t na oboch stranách, dostaneme,

△v = △a × △t (v čo je plocha pod krivkou v čase zrýchlenia graf )

• Pre objekt, ktorý sa pohybuje s konštantným zrýchlením, t.j. zrýchlenie je rovnaké vo všetkých časových intervaloch. Preto je sklon grafu zrýchlenia-čas nula a graf bude rovnobežný s časovou osou.

Akcelerácia vs retardácia

zrýchlenie: Zrýchlenie telesa sa označuje ako rýchlosť zmeny rýchlosti v danom časovom období. Je to vektorová veličina a meria sa v m/s².

Akcelerácia = zmena rýchlosti/času

tu je zmena rýchlosti pozitívna.

Predpokladajme, že teleso, ktoré sa pohybuje rovnomernou rýchlosťou, zvyšuje svoju rýchlosť. Rýchlosť zvyšovania rýchlosti sa označuje ako zrýchlenie telesa. Nech u je počiatočná rýchlosť, v je konečná rýchlosť a t je časový interval, potom je zrýchlenie telesa dané ako,

Zrýchlenie (a) = (v – u)/t

Príklad: Príkladom zrýchlenia v každodennom živote je otáčanie auta v zákrute. Rýchlosť auta sa zvyšuje so zmenou smeru, čo má za následok zrýchlenie. Zrýchlenie sa zvyšuje so zvyšujúcou sa rýchlosťou otáčania.

Retardácia: Retardácia telesa sa označuje ako rýchlosť zmeny rýchlosti v danom časovom období. Retardácia znamená negatívne zrýchlenie.

Retardácia = zmena rýchlosti/času

tu je zmena rýchlosti záporná.

Predpokladajme, že teleso, ktoré sa pohybuje rovnomernou rýchlosťou, svoju rýchlosť znižuje. Miera poklesu rýchlosti sa označuje ako retardácia telesa. Nech u je počiatočná rýchlosť, v je konečná rýchlosť a t je časový interval, potom je oneskorenie telesa dané ako,

Retardácia = (v – u)/t

Príklad: Reálnym príkladom retardácie je vypnutie ventilátora. Keď je vypínač pohyblivého ventilátora vypnutý, rýchlosť otáčania lopatiek ventilátora sa postupne spomaľuje. Táto miera zníženia rýchlosti ventilátora je známa ako retardácia.

Skontrolujte aj toto:

• Grafy vzdialenosti a času
• Grafy rýchlosti a času

Vzorové problémy na grafoch zrýchlenia

Problém 1: Z grafu zrýchlenia vs. času uvedeného nižšie určte zmenu rýchlosti.

Riešenie:

Aby sme našli zmenu rýchlosti telesa, musíme určiť plochu pod krivkou.

Aby sme teda našli zmenu rýchlosti objektu, musíme vypočítať plochu trojuholníka.

△v = plocha trojuholníka

= ½ × 25 × 6

△v = 75 m/s.

Zmena rýchlosti je teda 75 m/s.

Úloha 2: Z grafu zrýchlenia vs čas uvedeného nižšie nájdite počiatočnú rýchlosť telesa, ak je jeho konečná rýchlosť 55 m/s.

Riešenie:

Aby sme našli zmenu rýchlosti telesa, musíme určiť plochu pod krivkou. Z grafu môžeme pozorovať, že má obdĺžnik a trojuholník. Aby sme našli zmenu rýchlosti objektu, musíme vypočítať plochu týchto obrázkov.

△v = plocha trojuholníka + plocha obdĺžnika

= ½ × 8 × 6 + 2 × 8

△v = 24 + 16 = 42 m/s

My to vieme,

△v = konečná rýchlosť – počiatočná rýchlosť

42 = 55 – v_i

v_i= 55 – 42 = 13 m/s

Počiatočná rýchlosť je teda 13 m/s.

Problém 3: Z grafu zrýchlenia vs čas uvedeného nižšie určte rýchlosť v čase t = 6 sekúnd, ak v(0) = 0.

Riešenie:

Zrýchlenie je dané;

a = dv/dt

⇒ dv = (a)dt

Integráciou na oboch stranách dostaneme

∫dv = ∫(a) dt

⇒ v = ∫(1,5) dt

⇒ v(t) = 1,5t + c, kde c je konštanta

⇒ v(0) = 0

⇒ c = 0

Teraz, v(t) = 1,5t

v(6) = 1,5 x 6 = 9 m/s

Rýchlosť v čase t = 6 s je teda 9 m/s.

Problém 4: Čo označuje oblasť pod grafom zrýchlenia-čas?

Riešenie:

Oblasť pod grafom zrýchlenia-čas predstavuje zmenu rýchlosti.

Nech △v je zmena rýchlosti, △a je zmena zrýchlenia a △t je zmena v čase.

Teraz plocha pod krivkou = △v

Vieme, že zrýchlenie telesa sa označuje ako pomer zmeny rýchlosti v danom časovom úseku.

takže,

△a = △v/△t

Teraz, vynásobením s △t na oboch stranách, dostaneme,

△v = △a × △t

Takže plocha pod krivkou sa získa vynásobením zmeny zrýchlenia a zmeny v čase.

Problém 5: Čo znamená trhnutie v grafe času zrýchlenia?

Riešenie:

Trhnutie je náhla zmena zrýchlenia pohybujúceho sa telesa a sklon a-t grafu predstavuje trhnutie.

Strmosť grafu zrýchlenia-čas = trhnutie = △a/△t

Graf zrýchlenia – najčastejšie otázky

Čo je to graf zrýchlenia-čas?

Graf zrýchlenia a času zobrazuje, ako sa zrýchlenie mení v priebehu času pre objekt pohybujúci sa v priamke. Vykresľuje zrýchlenie na osi y proti času na osi x.

Ako vypočítate plochu pod grafom zrýchlenia a času a čo to predstavuje?

Oblasť pod grafom zrýchlenia-čas predstavuje zmenu rýchlosti za časové obdobie pokryté grafom. Na výpočet tejto plochy by ste zvyčajne spočítali plochy obdĺžnikov alebo lichobežníkov, ktoré sa zmestia pod krivku, čo zodpovedá odlišným časovým intervalom, počas ktorých je zrýchlenie konštantné​​.

Dokážete určiť rýchlosť objektu v konkrétnom čase z grafu zrýchlenia-čas?

Priame určenie okamžitej rýchlosti v konkrétnom čase z grafu zrýchlenia-čas nie je možné. Môžete však vypočítať zmenu rýchlosti za určité časové obdobie tak, že nájdete oblasť pod grafom v rámci tohto obdobia. Znalosť počiatočnej rýchlosti vám umožňuje určiť konečnú rýchlosť.

Čo znamená záporné zrýchlenie na tomto type grafu?

Záporné zrýchlenie na grafe zrýchlenia-čas označuje spomalenie, pri ktorom sa rýchlosť objektu znižuje, ak sa objekt pohybuje v kladnom smere. Ak sa objekt pohybuje v smere, ktorý sa považuje za negatívny, potom záporné zrýchlenie znamená zvýšenie rýchlosti.

Ako môžete nájsť priemerné zrýchlenie z grafu zrýchlenia-čas?

Priemerné zrýchlenie možno určiť nájdením celkovej zmeny rýchlosti (sčítaním plôch pod krivkou, zohľadnením smeru) a jej vydelením celkovým časovým intervalom. Vizuálne to možno znázorniť ako obdĺžnik, ktorého plocha je ekvivalentná celkovej ploche pod grafom zrýchlenia-čas.

Čo predstavuje sklon grafu zrýchlenia-čas?

Sklon grafu zrýchlenia-čas udáva rýchlosť zmeny zrýchlenia v priebehu času, čo je známe ako trhnutie. Strmý svah znamená rýchlu zmenu zrýchlenia.

Ako znázorníte telo v pokoji na grafe zrýchlenia a času?

Teleso v pokoji alebo pohybujúce sa konštantnou rýchlosťou je znázornené na grafe zrýchlenia-čas čiarou pozdĺž časovej osi pri nulovom zrýchlení.

Ako interpretujete graf zrýchlenia-čas?

Sklon grafu zrýchlenia-čas predstavuje rýchlosť zmeny zrýchlenia, pričom strmší sklon indikuje vyššiu rýchlosť zmeny.

Čo predstavuje oblasť pod grafom zrýchlenia-čas?

Oblasť pod krivkou na grafe zrýchlenia-čas predstavuje zmenu rýchlosti objektu. Konkrétne predstavuje konečnú rýchlosť mínus počiatočnú rýchlosť.